一级倒立摆的Simulink仿真

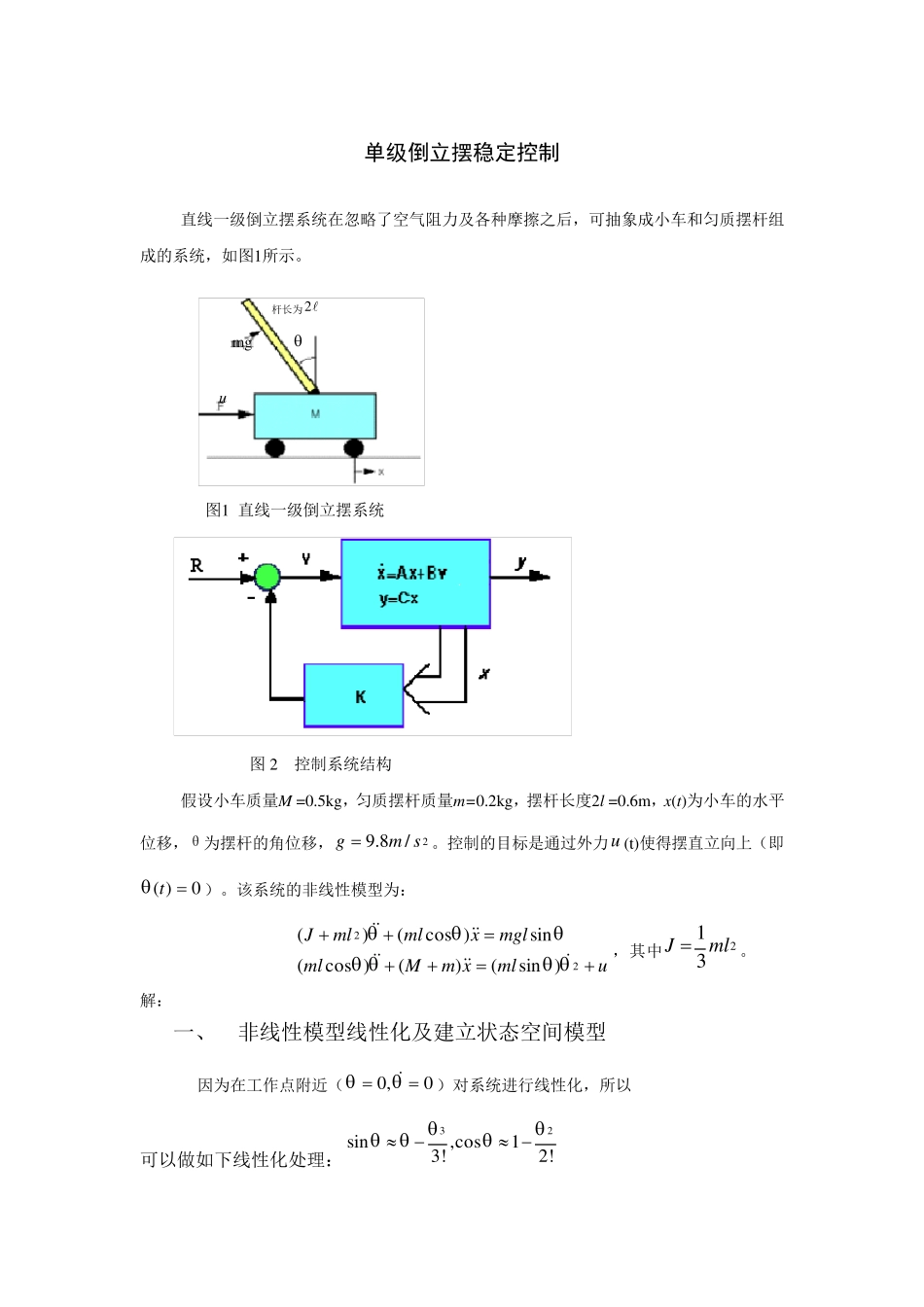
单级倒立摆稳定控制 直线一级倒立摆系统在忽略了空气阻力及各种摩擦之后，可抽象成小车和匀质摆杆组成的系统，如图1所示。 mg杆长为2u 图1 直线一级倒立摆系统 图2 控制系统结构 假设小车质量M =0.5kg，匀质摆杆质量m=0.2kg，摆杆长度2l =0.6m，x(t)为小车的水平位移，θ为摆杆的角位移，2/8.9smg 。控制的目标是通过外力u (t)使得摆直立向上（即0)(t）。该系统的非线性模型为： umlxmMmlmglxmlmlJ22)sin()()cos(sin)cos()(，其中231mlJ 。 解： 一、 非线性模型线性化及建立状态空间模型 因为在工作点附近（0,0）对系统进行线性化，所以 可以做如下线性化处理：32sin,cos13!2!  当θ 很小时，由cosθ、sinθ 的幂级数展开式可知，忽略高次项后， 可得 cosθ≈1，sinθ≈θ，θ’^2≈0； 因此模型线性化后如下： （J+ml^2）θ’’+mlx’’=mglθ (a) mlθ’’+(M+m) x’’=u (b) 其中231mlJ  取系统的状态变量为,,,,4321xxxxxx输出Txy][包括小车位移和摆杆的角位移. 即 X=4321xxxx=''xx Y=x =31xx 由线性化后运动方程组得 X1’=x’=x2 x2’=x’’=mmMmg3)(43x3+mmM3)(44u X3’ =θ’=x4 x4’=θ’’=mllmMgmM3)(4)(3x3+mllmM3)(43u 故空间状态方程如下： X’='4'3'2'1xxxx=03)(4)(300100003)(43000010mllmMgmMmmMmg 4321xxxx + mllmMmmM3)(4303)(440 u X’='4'3'2'1xxxx=01818.3100100006727.2000010 4321xxxx +  5455.408182.10 u Y= 31xx=01000001 4321xxxx 二、通过 Matlab 仿真判断系统的可控与可观性，并说明其物理意义。 （1）判断可控性 代码： A=[0 1 0 0; 0 0 -2.627 0; 0 0 0 1; 0 0 31.1818 0]; B=[0;1.8182;0;-4.5455]; P=ctrb(A,B); n=rank(P); 运行了得 n= 4 所以 P 为满秩，系统能控 （2）判断可观性...