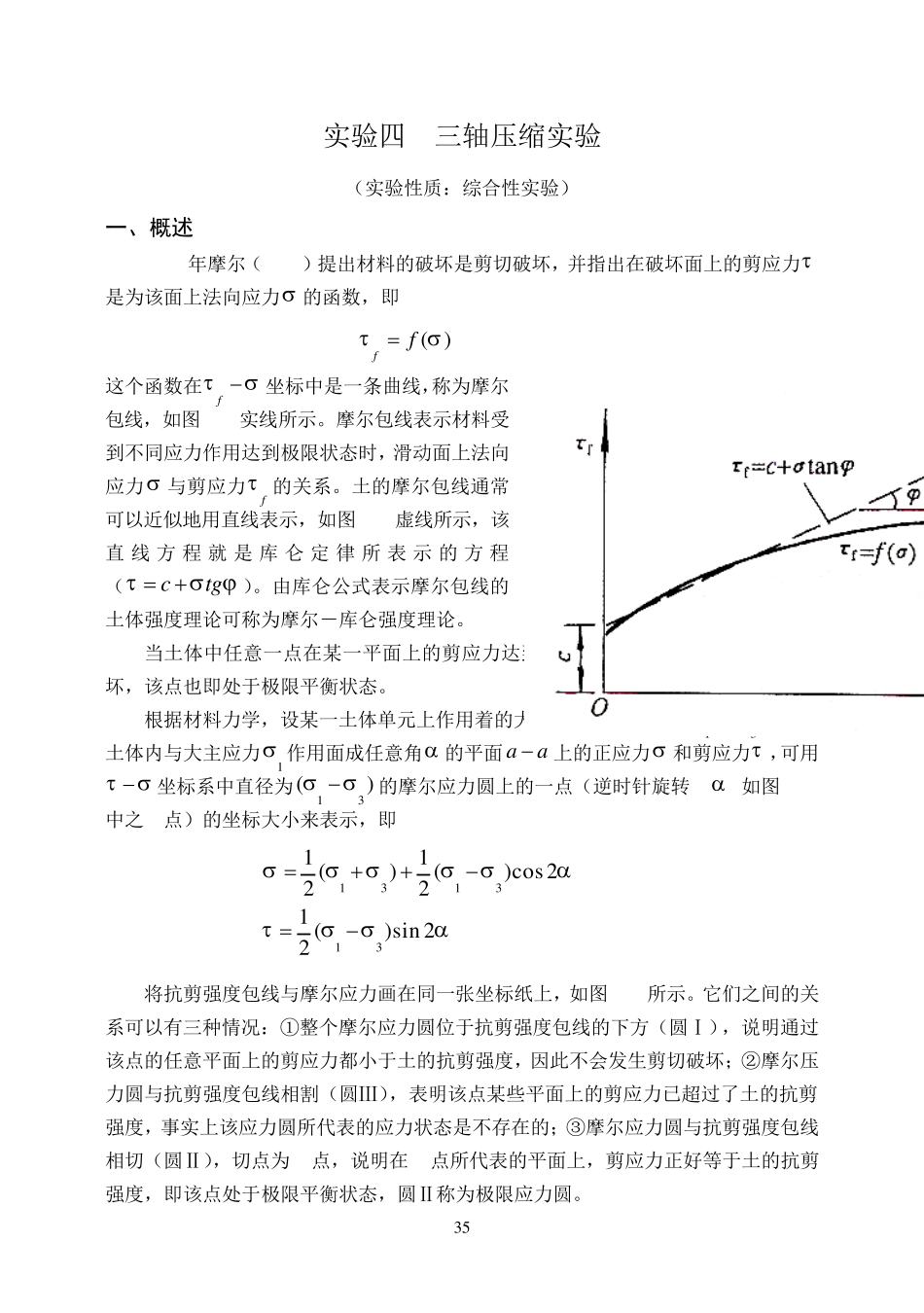
35 实验四 三轴压缩实验 (实验性质:综合性实验) 一、概述 1910年摩尔(Mohr)提出材料的破坏是剪切破坏,并指出在破坏面上的剪应力是为该面上法向应力 的函数,即 ( )ff 这个函数在f坐标中是一条曲线,称为摩尔包线,如图 4-1实线所示。摩尔包线表示材料受到不同应力作用达到极限状态时,滑动面上法向应力 与剪应力f 的关系。土的摩尔包线通常可以近似地用直线表示,如图 4-1虚线所示,该直 线 方 程 就 是 库 仑 定 律 所 表 示 的 方 程(ctg )。由库仑公式表示摩尔包线的土体强度理论可称为摩尔-库仑强度理论。 图 4-1 摩尔包线 当土体中任意一点在某一平面上的剪应力达到土的抗剪强度时,就发生剪切破坏,该点也即处于极限平衡状态。 根据材料力学,设某一土体单元上作用着的大、小主应力分别为1 和3 ,则在土体内与大主应力1 作用面成任意角 的平面 aa上的正应力 和剪应力 ,可用坐标系中直径为13()的摩尔应力圆上的一点(逆时针旋转2 ,如图 4-2中之A点)的坐标大小来表示,即 13131311()()cos2221 ()sin 22 将抗剪强度包线与摩尔应力画在同一张坐标纸上,如图 4-3所示。它们之间的关系可以有三种情况:①整个摩尔应力圆位于抗剪强度包线的下方(圆Ⅰ),说明通过该点的任意平面上的剪应力都小于土的抗剪强度,因此不会发生剪切破坏;②摩尔压力圆与抗剪强度包线相割(圆Ⅲ),表明该点某些平面上的剪应力已超过了土的抗剪强度,事实上该应力圆所代表的应力状态是不存在的;③摩尔应力圆与抗剪强度包线相切(圆Ⅱ),切点为 A点,说明在 A点所代表的平面上,剪应力正好等于土的抗剪强度,即该点处于极限平衡状态,圆Ⅱ称为极限应力圆。 3 6 图4-2 用摩尔圆表示的土体中任意点的应力 图4-3 摩尔圆与抗剪强度包线之间的关系 三轴压缩实验(亦称三轴剪切实验)是以摩尔-库仑强度理论为依据而设计的三轴向加压的剪力试验,试样在某一固定周围压力3 下,逐渐增大轴向压力1 ,直至试样破坏,据此可作出一个极限应力圆。用同一种土样的3~4个试件分别在不同的周围压力3 下进行实验,可得一组极限应力圆,如图4-4中的圆Ⅰ、圆Ⅱ和圆Ⅲ。作出这些极限应力圆的公切线,即为该土样的抗剪强度包络线,由此便可求得土样的抗剪强度指标。 图4-4 三轴实验基本原理 a)试样承受3 ...