传热学大作业报告二维稳态导热

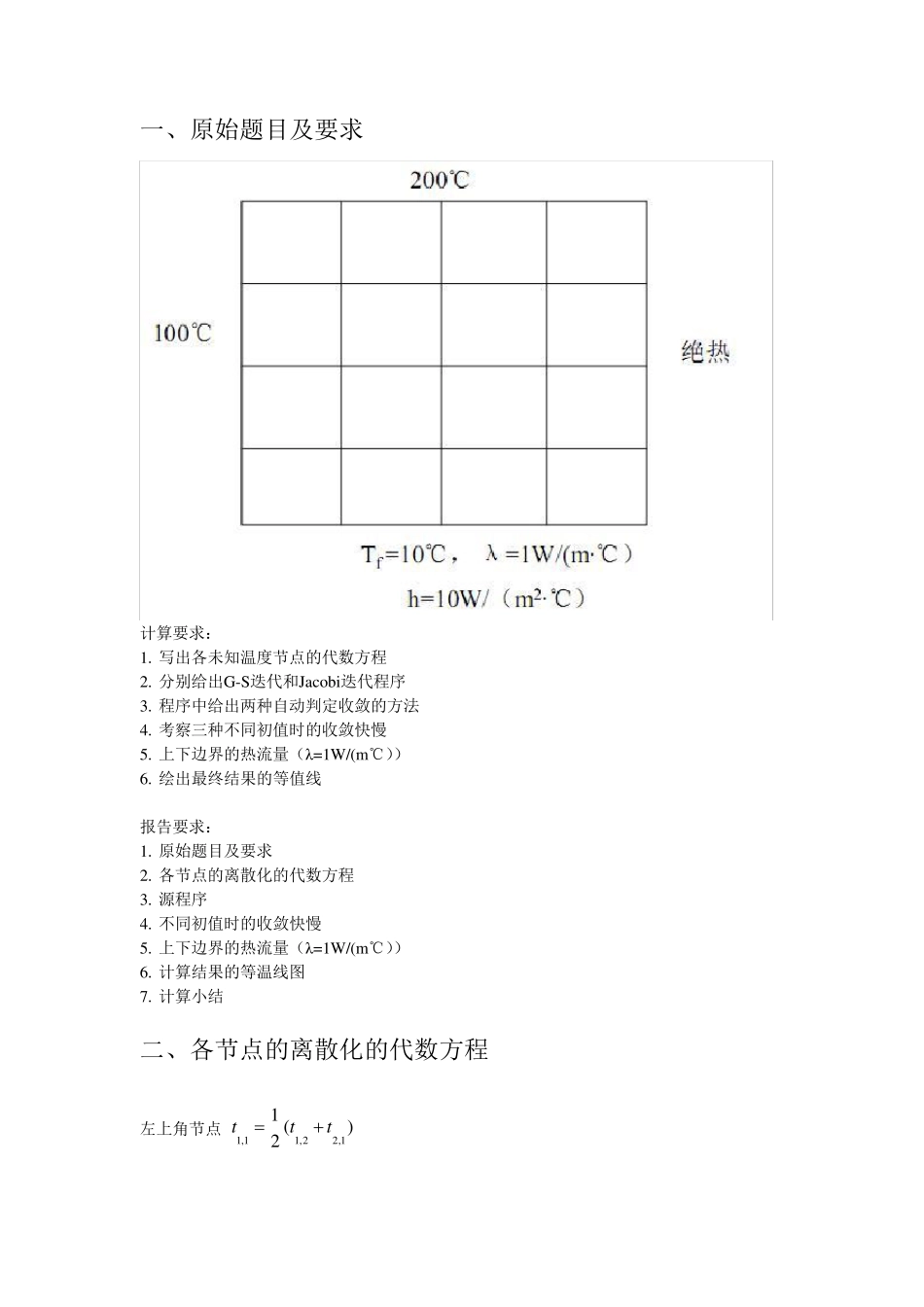
传热学大作业报告 二维稳态计算 院系：能源与环境学院 专业：核工程与核技术 姓名：*** 学号：******** 一、原始题目及要求 计算要求： 1. 写出各未知温度节点的代数方程 2. 分别给出G-S迭代和Jacobi迭代程序 3. 程序中给出两种自动判定收敛的方法 4. 考察三种不同初值时的收敛快慢 5. 上下边界的热流量（λ=1W/(m℃）） 6. 绘出最终结果的等值线 报告要求： 1. 原始题目及要求 2. 各节点的离散化的代数方程 3. 源程序 4. 不同初值时的收敛快慢 5. 上下边界的热流量（λ=1W/(m℃）） 6. 计算结果的等温线图 7. 计算小结 二、各节点的离散化的代数方程 左上角节点 )(211,22,11,1ttt 右上角节点 )(215,24,15,1ttt 左下角节点 Ct1 0 01,5 右下角节点 )2(211,24,55,5xhttxht 左边界节点 Cti1 0 01,， 42 i 上边界节点 Ctj 2 0 0,1， 42 j 右边界节点 )2(415,15,14,5,iiiitttt， 42 i 下边界节点 )42()2(211,51,5,4,5txhtttxhtjjjj， 42 j 内部节点 )(21,1,11,1,,jijijijijittttt，4,2ji 三、源程序 1 、G-S迭代法 t=zeros(5,5); t0=zeros(5,5); dteps=0.0001; for i=2:5 %左边界节点 t(i,1)=100; end for j=2:4 %上边界节点 t(1,j)=200; end t(1,1)=(t(1,2)+t(2,1))/2; t for k=1:100 for i=2:4 %内部节点 for j=2:4 t(i,j)=(t(i-1,j)+t(i+1,j)+t(i,j-1)+t(i,j+1))/4; end end t(1,5)=(t(1,4)+t(2,5))/2;%右上角节点 for i=2:4;%右边界节点 t(i,5)=(2*t(i,4)+t(i-1,5)+t(i+1,5))/4; end for j=2:4; %下边界节点 t(5,j)=(2*t(4,j)+t(5,j-1)+t(5,j+1)+200)/24; end t(5,5)=(t(5,4)+t(4,5)+100)/12;%右下角节点 dtmax=0; for i=1:5 for j=1:5 dtmax=max(abs(t(i,j)-t0(i,j)),dtmax); end end k t dtmax t0=t; contour(t',30); pause; if dtmax