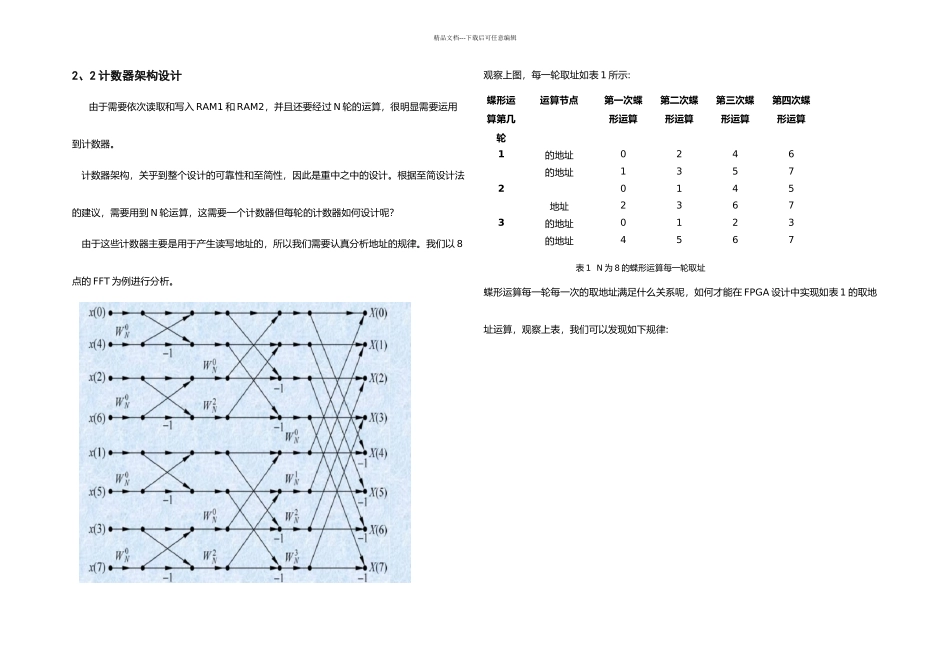
精品文档---下载后可任意编辑1、 DIT-FFT 算法的基本原理有限长序列的 N 点 DFT 定义为:,式中。DFT 在实际应用中很重要,但是假如直接按 DFT 变换进行计算,当序列长度 N 很大时,计算量会非常大,所需时间也很长,因此常用的是 DFT 的一种快速计算算法,简称 FFT。最常用的 FFT 算法是基于时间抽取的基 2-FFT 算法和基于频率抽取的基 2-FFT 算法,这种算法的特点在于 FFT 会把一次大的 DFT 分割成几个小的 DFT,这样递归式地细分下去,例如有 8 个采样点的 FFT,首先会把最外层的 8 点运算分成两个 4 点 FFT 的奇偶组合,第二层FFT 又分成四个两点 FFT 的奇偶组合,并且由此计算出的频谱中很有趣的一点在于对于实数输出的数组,后面一半和前面一半正好对称相同,对于虚数输出的数组,后面一半是前面数组对称后乘上负 1,因此,我们只需要算出 FFT 的一半即可求出全部。本设计讨论的是基于至简设计法实现按时间抽选的基 2-FFT 算法(即 DIF-FFT)实现过程,支持 N 由 8 到 1024。图 1 按时间抽取的基 2-FFT 算法蝶形运算流图(N=8)2、 蝶形运算至简实现过程2、1 模块划分图 2 蝶形运算模块框图本模块包括三个 RAM 模块(RAM1,RAM2,RAM3)与一个 DFT 模块,各模块功能如下:1) RAM1 模块:在开始进行蝶形运算前,全部采样点(如图 1 所示的精品文档---下载后可任意编辑x(0)、x(4)、x(2)、x(6)、x(1)、x(5)、x(3)、x(7))已经根据倒位序二进制的地址依次存储在 RAM1 模块中,即地址 0 保存了采样点 x(0),地址 1 保存了采样点 x(4)。选用双端口 RAM1 可以同时对两点采样数据(如图 1 的 x(0)、x(4))进行读、写操作。2)RAM2 模块:RAM2 模块也是采纳双端口输入输出,可同时对两点数据进行读、写操作。3)DFT 模块:DFT 模块用于对 RAM1、RAM2 输出的两点采样数据(如图 1 的x(0)、x(4))进行蝶形运算,它将运算结果输出至 RAM1、RAM2 模块进行保存。4)RAM3 模块:RAM3 模块是单输出模块,理论是应保存 N(N 为采样点个数)个运算参数,但由于每一次蝶形运算结果,)具有对称性,因此 RAM3 只需要保存 N/2 个即可。2、1、1 奇数轮蝶形运算 图 3 第奇数轮蝶形运算流图如图 3 所示,RAM1 首先根据计数器给出的两个点的地址(如地址 0,地址 1)进行数据读操作,然后将数据(如和)送进 DFT 模块进行运算,最后 RAM2 将 DFT 模...