历年全国初中数学联赛试题总汇

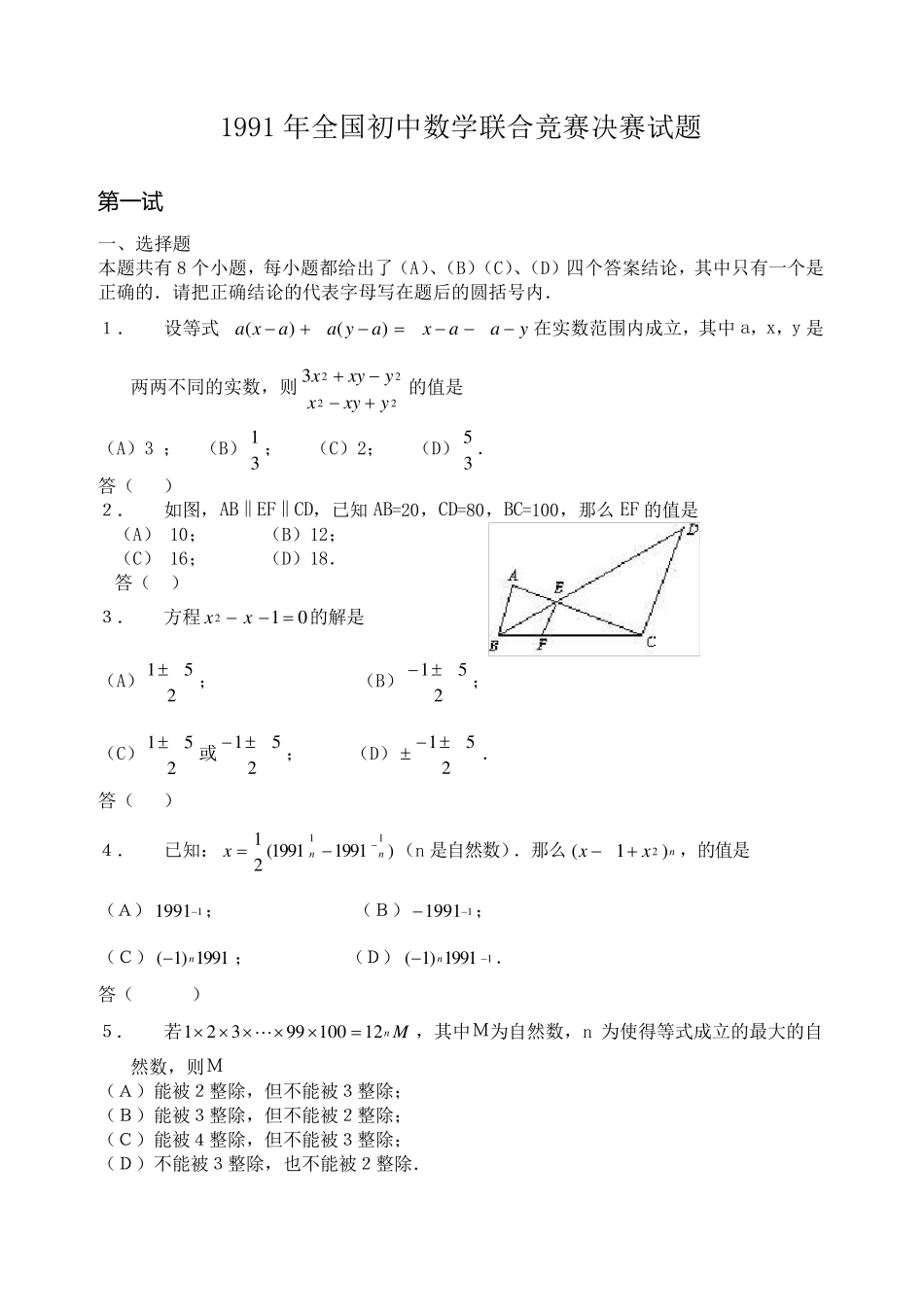
1991 年全国初中数学联合竞赛决赛试题 第 一试 一、选择题 本题共有8 个小题，每小题都给出了（A）、（B）（C）、（D）四个答案结论，其中只有一个是正确的．请把正确结论的代表字母写在题后的圆括号内． １． 设等式yaaxayaaxa)()(在实数范围内成立，其中a，x，y 是两两不同的实数，则22223yxyxyxyx的值是 （A）3 ； （B）31 ； （C）2； （D）35 ． 答（ ） ２． 如图，AB‖EF‖CD，已知 AB=20，CD=80，BC=100，那么 EF 的值是 （A） 10； （B）12； （C） 16； （D）18． 答（ ） ３． 方程012 xx的解是 （A）251 ； （B）251 ； （C）251 或251 ； （D）251 ． 答（ ） ４． 已知：)19911991(2111nnx（n 是自然数）．那么nxx)1(2，的值是 （Ａ）11 9 9 1  ； （Ｂ） 11 9 9 1 ； （Ｃ）1991)1(n； （Ｄ）11991)1(n． 答（ ） ５． 若Mn1 21 0 09 9321，其中Ｍ为自然数，n 为使得等式成立的最大的自然数，则Ｍ （Ａ）能被２整除，但不能被３整除； （Ｂ）能被３整除，但不能被２整除； （Ｃ）能被４整除，但不能被３整除； （Ｄ）不能被３整除，也不能被２整除． 答（ ） ６． 若a，c，d 是整数，b 是正整数，且满足 cba， dcb， adc，那么 dcba的最大值是 （Ａ）1 ；（Ｂ）5 ；（Ｃ）0 ；（Ｄ）１． 答（ ） ７． 如图，正方形OPQR内接于ΔABC．已知ΔAOR、ΔBOP 和ΔCRQ 的面积分别是11 S，32 S和13 S，那么，正方形OPQR的边长是 （Ａ）2 ；（Ｂ）3 ；（Ｃ）2 ；（Ｄ）3． 答（ ） ８． 在锐角ΔABC 中，1AC，cAB ，60 A，ΔABC的外接圆半径R ≤1，则 （Ａ）21 < c < 2 ； （Ｂ）0< c ≤ 21 ； 答（ ） （C）c > 2； （D）c = 2． 答（ ） 二、填空题 １．Ｅ是平行四边形ABCD中 BC 边的中点，AE 交对角线 BD 于G，如果ΔBEG 的面积是１，则平行四边形ABCD的面积是 ． ２．已知关于x 的一元二次方程02cbxax没有实数解．甲由于看错了二次项系数，误求得两根为２和４；乙由于看错了某一项系数的符号，误求得两根为－１和４，那么，acb32 ． 3．设 m，n，p，q 为非负数，且对一切 x >０，qpnmxxxx)1(1)1(恒成立，则 qpnm22)2( ． ...