双向板支承梁参考资料

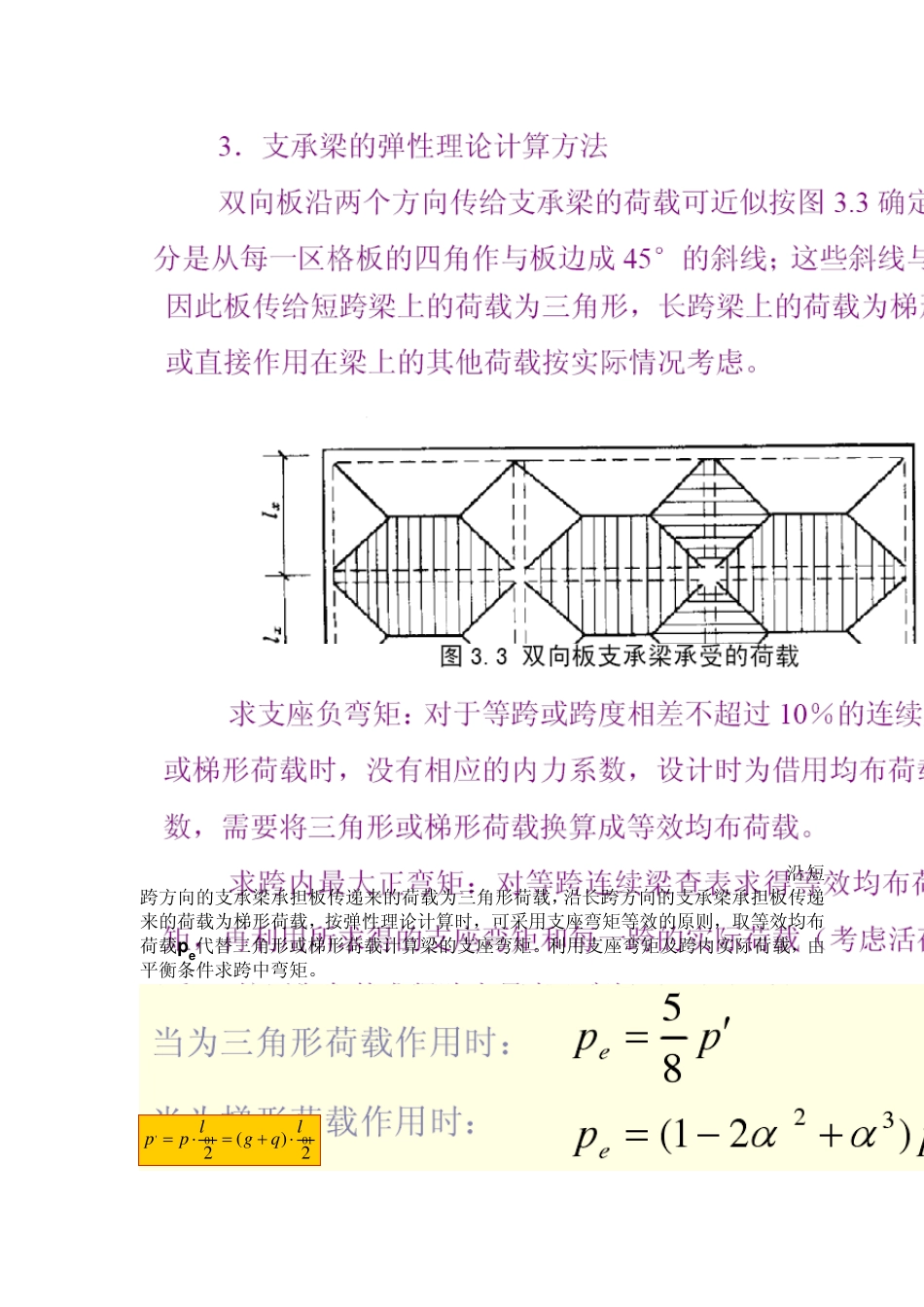
沿短跨方向的支承梁承担板传递来的荷载为三角形荷载，沿长跨方向的支承梁承担板传递来的荷载为梯形荷载，按弹性理论计算时，可采用支座弯矩等效的原则，取等效均布荷载pe代替三角形或梯形荷载计算梁的支座弯矩。利用支座弯矩及跨内实际荷载，由平衡条件求跨中弯矩。 '0 10 1()22llppgq按塑性理论计算支承梁时，可在弹性理论计算求得的支座弯矩基础上，应用调幅法确定支座截面弯矩值，然后按实际荷载根据静力平衡条件求出跨中弯矩。 三、支承梁的设计 按弹性理论设计支承梁。双向板支承梁承受的荷载如图四所示。计算梁的内力，进行梁的正截面、斜截面承载力计算，并对此梁进行钢筋配置。 图四 双向板支承梁承受的荷载 1.纵向支承梁 L -1 设计 1)跨度计算 边跨： 110 .3 70 .450 .1 8 50 .2522nabllm 11 .0 2 51 .0 2 5(50 .1 8 50 .2 )0 .24 .9 32nblm 取小值14 .9 3lm。 中跨： 取支乘中心线间的距离25 .0lm， 平均跨度： (4 .9 35 .0 ) / 24 .9 6 5 m, 按等跨连续梁计算。 2)荷载计算 由板传来的恒荷载的设计值： 1 .23 .7 6 552 7 .1 1/gkNm 由板传来的活荷载的设计值： 1 .3453 1 .2/qkNm  梁自重： 0 .2 5(0 .4 50 .1 )2 53 .1 2 5/kNm； 梁自重均布荷载设计值： 1 .23 .1 2 53 .7 5/gkNm。 纵向支承梁的计算图如图五所示。 图五 3 )内力计算 将g’、q’转化为均布荷载： 552 7 .1 11 6 .9 4/88ggkN m 553 1 .21 9 .5/88qqkNm a) 弯矩计算：222102030Mk glk g lk q l (k值由附表查得 )。 边跨: 2203 .7 54 .9 39 1 .1 4glkN m 2201 6 .9 44 .9 34 1 1 .7 3g lkN m 2201 9 .54 .9 34 7 3 .9 5q lkN m 中跨: 2203 .7 559 3 .7 5glkN m 2201 6 .9 454 2 3 .5g lkN m 2201 9 .554 8 7 .5q lkN m 平均跨： 2203 .7 54 .9 6 59 2 .4 4glkN m 2201 6 .9 44 .9 6 54 1 7 .5 9g lkN m 2201 9 .54 .9 6 54 8 0 .7q lkN m 纵向梁弯矩计算如表所示 表 4 纵向支承梁 L-1弯矩计算表 ...