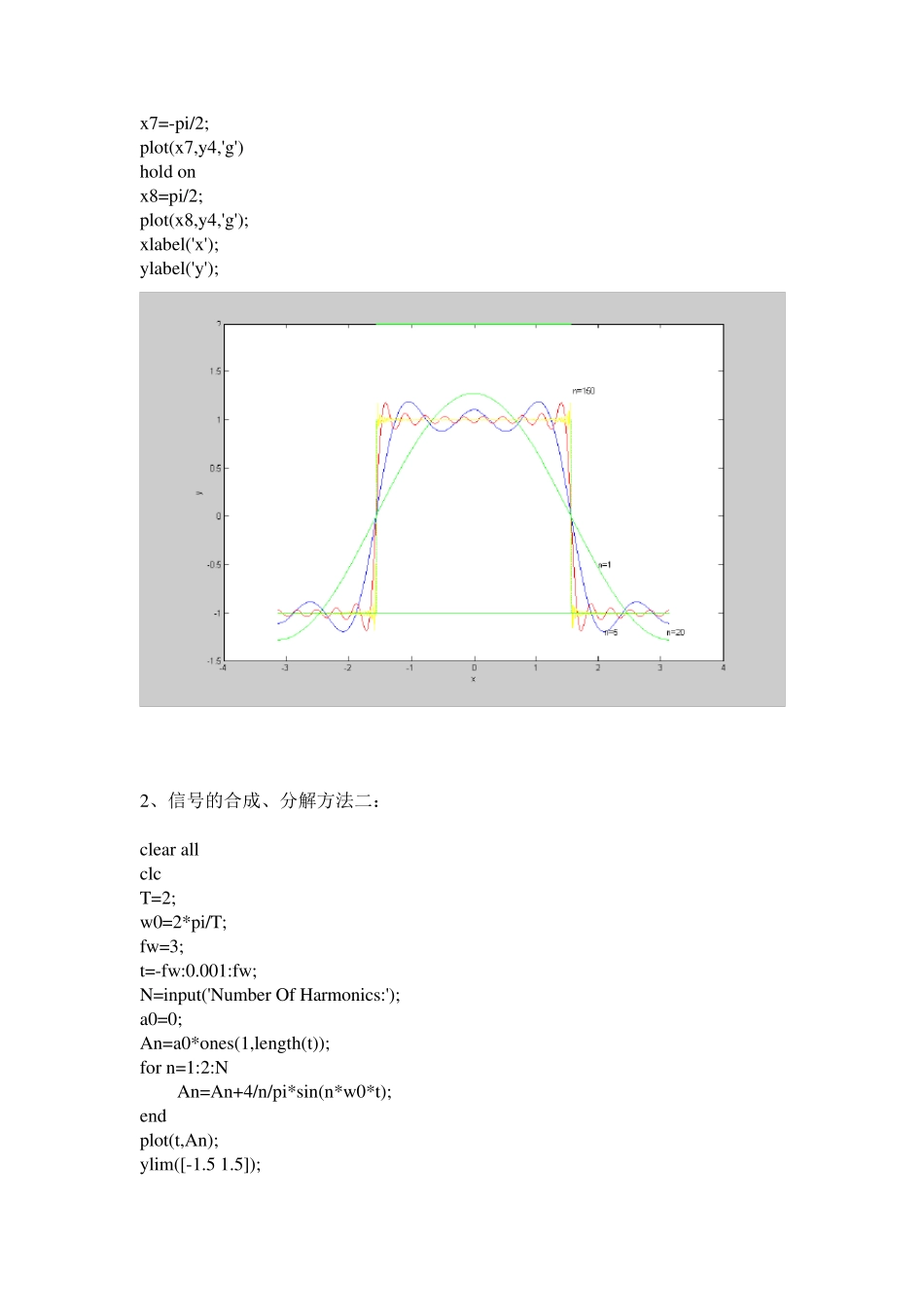
广东工业大学实验报告 信息工程学院 成绩评定_______ 学号: 姓名: 教师签名_______ 预习情况 操作情况 考勤情况 数据处理情况 实验4 题目:周期信号的合成与分解 第7 周 星期3 第 8、9 节 一、实验目的 1.熟悉信号的合成、分解原理,加深对傅立叶级数的理解; 2.了解和认识吉布斯现象(Gibbs)。 一、 实验原理 信号可以分解为一个直流分量和许多不同频率的正弦分量之和。主要表现各频率的正弦分量在信号所占比重大小的不同。 根据周期信号的傅立叶级数展开式可知,任何非正弦周期信号,只要满足狄里赫利条件都可以分解为一直流分量和由基波及各次谐波(基波的整数倍)分量的叠加。 同样,由基波及各次谐波分量也可以叠加出一个周期方波信号。至于叠加出来的信号与原信号的误差,则取决于傅立叶级数的项数。根据傅立叶的原理,任何周期信号都可以分解为用一组三角函数{sin(tnf02),cos(tnf02)}的组合表示。 合成波形所包含的谐波分量越多,除间断点附近外,它越接近于原方波信号,在间短点附近,随着所含谐波次数增 高 ,合成波形的尖 峰 越靠 近间断点,但 尖 峰 幅度 并 未 明 显 减 小,即 当 合成波形包含的谐波次数n,在间断点附近仍 有 9%的偏 差,这 种 现象称 为吉布斯现象(Gibbs)。 二 、 验证 性 实验 1、信号的合成、分解方法 一: clear all clc x0=-pi:0.01:pi; sum=0.0; for(n0=1:1:5) p0=4*sin(n0*pi/2)*cos(n0*x0)/(n0*pi); sum=sum+p0; end plot(x 0,su m,'b') tex t(2.1,-1.2,'n=5') hold on; x 1=-pi:0.01:pi; su m=0.0; for(n1=1:1:20) p1=4*sin(n1*pi/2)*cos(n1*x 1)/(n1*pi); su m=su m+p1; end plot(x 1,su m,'r') tex t(3.1,-1.2,'n=20') hold on; x 2=-pi:0.01:pi; su m=0.0; for(n2=1:1:150) p2=4*sin(n2*pi/2)*cos(n2*x 2)/(n2*pi); su m=su m+p2; end plot(x 2,su m,'y ') tex t(1.6,1.3,'n=150') hold on; x 3=-pi:0.01:pi; su m=0.0; for(n3=1) p3=4*sin(n3*pi/2)*cos(n3*x 3)/(n3*pi); su m=su m+p3; end plot(x 3,su m,'g') tex t(2,-0.5,'n=1') hold on; x 4=-pi:0.01:pi/2; y 1=-1; plot(x 4,y 1,'g') hold on x 5=-pi/2:0.01:pi/2; y 2=2; plot(x 5,y 2,'g') hold on x 6=pi/2:0.01:pi; y 3=-1; plot(x 6,y 3,'g') hold on y...