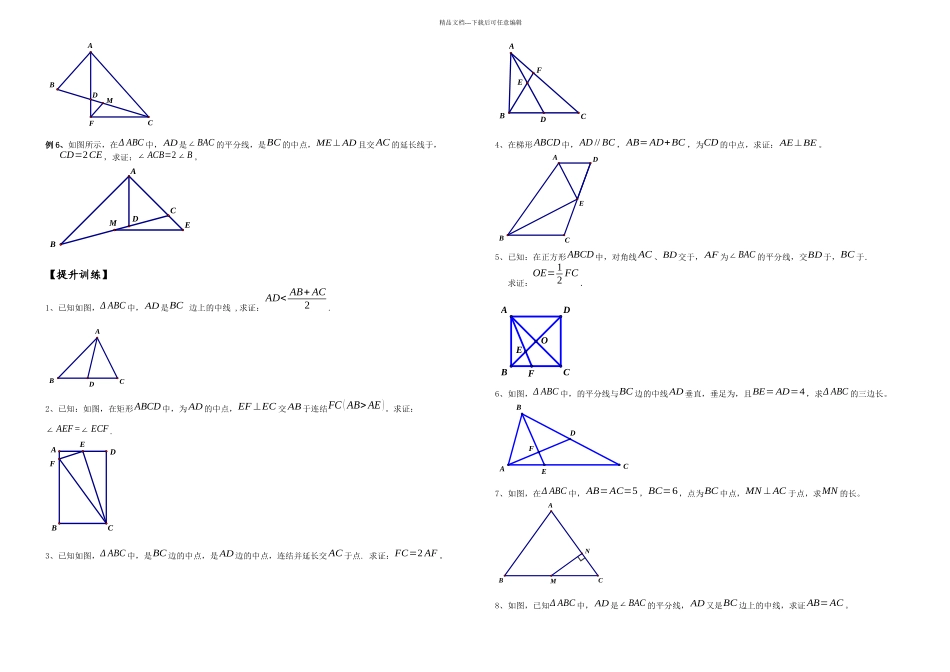
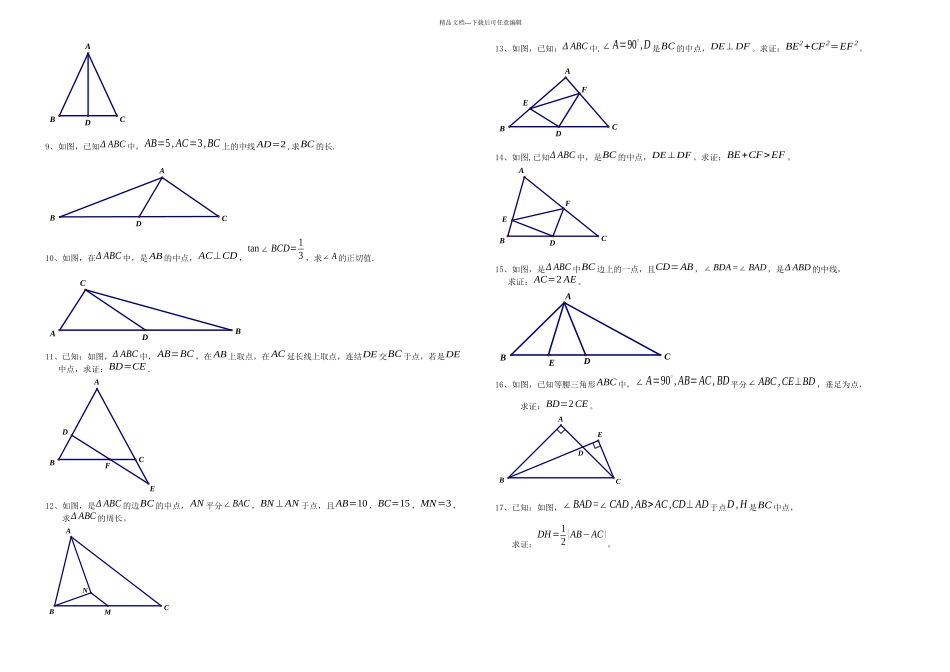
精品文档---下载后可任意编辑【知识要点】1、中位线定理:如图,在中,若,,则且。2、中线倍长(倍长中线):如图(左图),在中,为中点,延长到使,连接,则有:≌。作用:转移线段和角。注意:① 在实际运用中,与某个中点相连的线段,都可以将其看作“中线”,从而都可以考虑将它倍长(需要的话)。② 如上右图,假如出现“两条平行线夹中点”的情形,一定会出现“X 全等”或“叉叉全等”或“8 字型全等”,有时这个“叉叉”需要我们自己画出来(辅助线).3、直角三角形斜边中线定理:如图,在中,,为中点,则有:。4、三线合一:在中:(1);(2)平分;(3),(4).“知二得二”:比如由(2)(3)可得出(1)(4).也就是说,以上四条语句,任意选择两个作为条件,就可以推出剩下两条。请牢记:当你发现有某一条线同时具备了“垂线”、“角平分线”、“中线”三种功能当中的任意两种功能时,那么这条线就一定是某个等腰三角形的对称轴,换句话说,以这条线为对称轴必定有等腰三角形出现.【经典例题】例 1、如图所示,已知为BC 中点,点在DE 上,且AB=CE ,求证:∠BAD=∠CED .例 2、如图,已知在Δ ABC 中,AD 是BC 边上的中线,是AD 上一点,且BE= AC ,延长交AC 于,求证:AF=EF 。例 3、如图,在中,AD 为的平分线,为BC 的中点,AD // ME ,求证:BE=CF=12(AB+ AC )。例 4、如图,已知Δ ABC 中,BD,CE 为高线,点是DE 的中点,点是BC 的中点.求证:MN ⊥DE 。例 5、如图所示,在P,PD⊥BM中,D ,为BC 的中点,AD 是∠BAC 的平分线,若CF ⊥ AD 且交AD 的延长线于,求证:F。EDABCABCEDDMCBACBADDABCADBCEFEDBCAFEDMBCANMDEBCA精品文档---下载后可任意编辑例 6、如图所示,在Δ ABC 中,AD 是∠BAC 的平分线,是BC 的中点,ME⊥ AD 且交AC 的延长线于,CD=2CE ,求证:∠ ACB=2∠B 。【提升训练】1、已知如图,Δ ABC 中,AD 是BC 边上的中线 ,求证:AD< AB+ AC2.2、已知:如图,在矩形ABCD 中,为AD 的中点,EF ⊥EC 交AB 于连结FC ( AB> AE )。求证:∠ AEF =∠ ECF . 3、已知如图,Δ ABC 中,是BC 边的中点,是AD 边的中点,连结并延长交AC 于点. 求证:FC=2 AF 。4、在梯形ABCD 中,AD // BC ,AB= AD+BC ,为CD 的中点,求证:AE⊥BE 。5、已知:在正方形ABCD 中,对角线AC 、BD交于,AF 为∠BAC 的平分线,交BD于,BC 于....