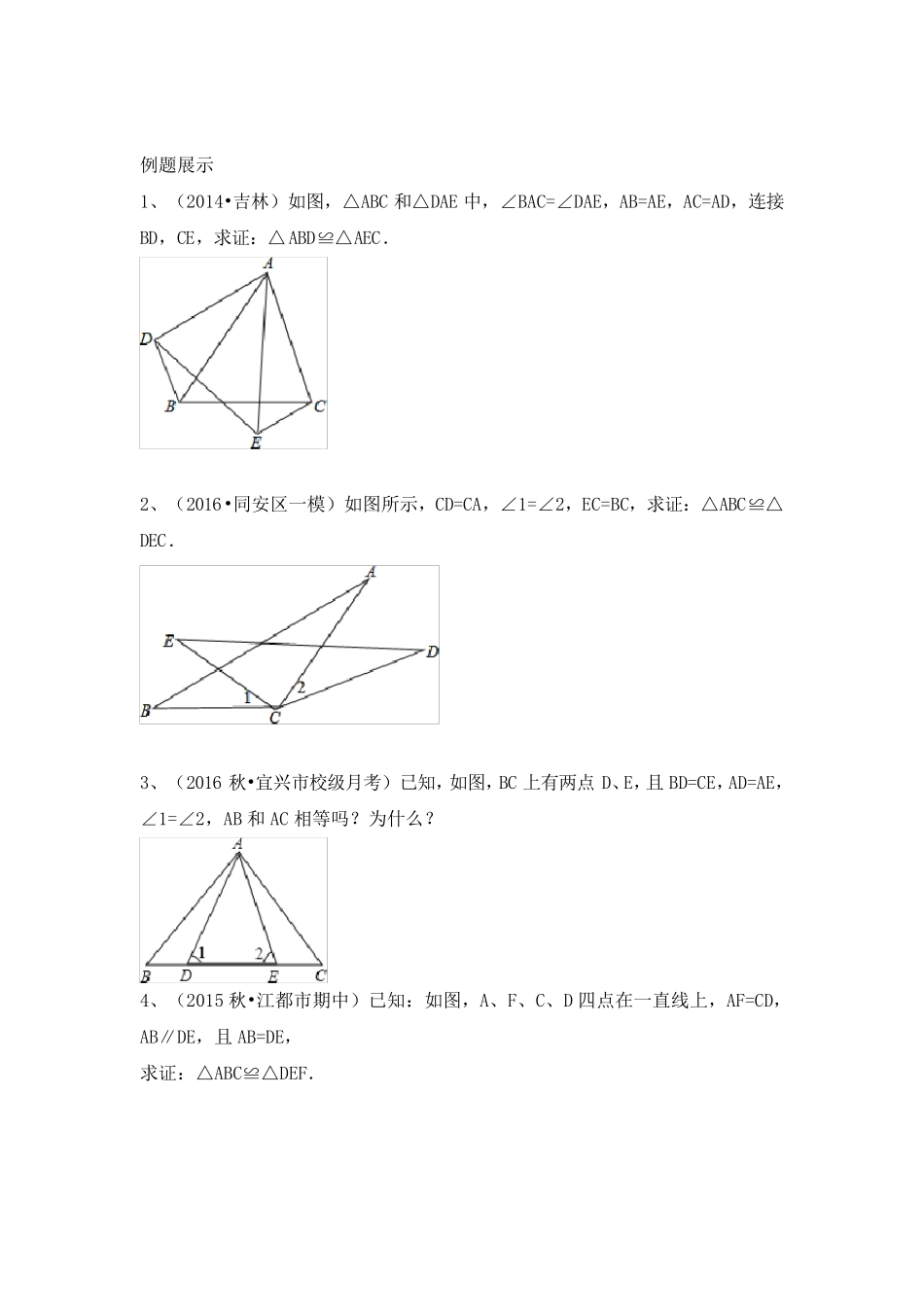
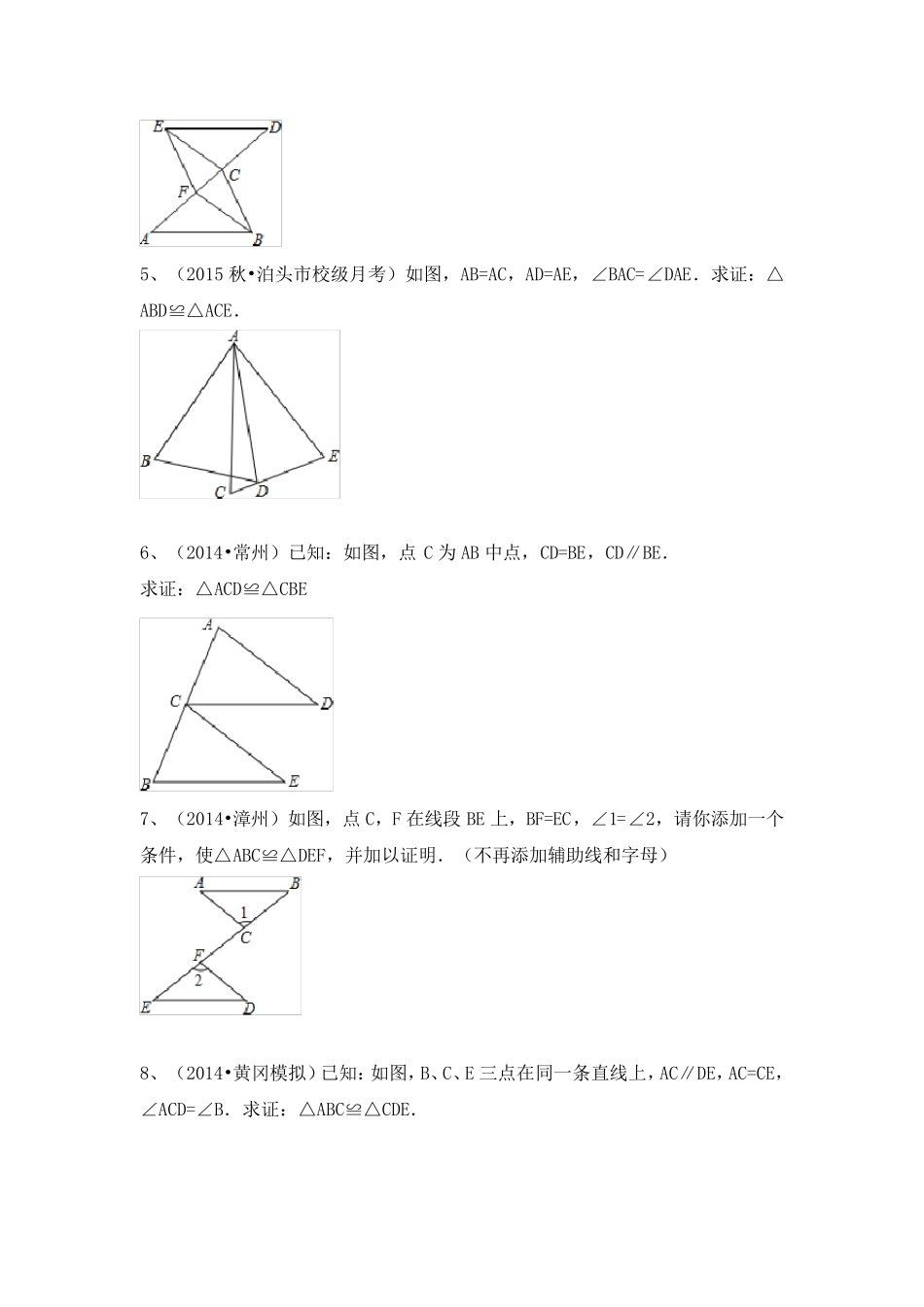
全等三角形的判定(SAS) 一、常用的知识点 1、全等三角形的性质: 对应边相等,对应角相等 对应边上的高相等 对应边上的中线相等 对应角的角平分线相等 周长相等 面积相等 2、等腰直角三角形的性质: 两锐角互余,相等,且等于45 。 3、等边三角形的性质: 三条边相等,三个角相等并且等于60 。 4、任意三角形三边的关系: 另外两边之差的绝对值 第三边 另外两边之和 5、三角形的内角和定理: 三角形的内角和等于180 。 6、关于三角形的外角的推论: 三角形的外角等于其不相邻两内角和。 7、 关于公共角公共边的问题 ①(公共角问题)若CAEBAD,则EADBAC ? 为什么 ? ②(公共边问题)若AFDC ,则ACBF ? 为什么 ? 例题展示 1、(2014•吉林)如图,△ABC 和△DAE 中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证:△ABD≌△AEC. 2、(2016•同安区一模)如图所示,CD=CA,∠1=∠2,EC=BC,求证:△ABC≌△DEC. 3、(2016 秋•宜兴市校级月考)已知,如图,BC 上有两点 D、E,且 BD=CE,AD=AE,∠1=∠2,AB 和AC 相等吗?为什么? 4、(2015 秋•江都市期中)已知:如图,A、F、C、D 四点在一直线上,AF=CD,AB∥DE,且 AB=DE, 求证:△ABC≌△DEF. 5、(2015 秋•泊头市校级月考)如图,AB=AC,AD=AE,∠BAC=∠DAE.求证:△ABD≌△ACE. 6、(2014•常州)已知:如图,点 C 为 AB 中点,CD=BE,CD∥BE. 求证:△ACD≌△CBE 7、(2014•漳州)如图,点 C,F 在线段 BE 上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母) 8、(2014•黄冈模拟)已知:如图,B、C、E 三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.求证:△ABC≌△CDE. 9、(2014•房县三模)如图,C 是线段AB 的中点,CD 平分∠ACE,CE 平分∠BCD,CD=CE. 求证:△ACD≌△BCE 10、(2013 秋•合浦县期末)如图,A、D、F、B 在同一直线上,AD=BF,AE=BC,且 AE∥BC.求证:△AEF≌△BCD. 11、(2014 春•工业园区期末)已知:如图,BC∥EF,AD=BE,BC=EF,试说明△ABC≌△DEF. 12、(2013 •云南)如图,点B 在AE 上,点D 在AC 上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个). (1)你添加的条件是 . (2)添加条件后,请说明△ABC≌△ADE 的理由 13、(2012 秋•台州期中...