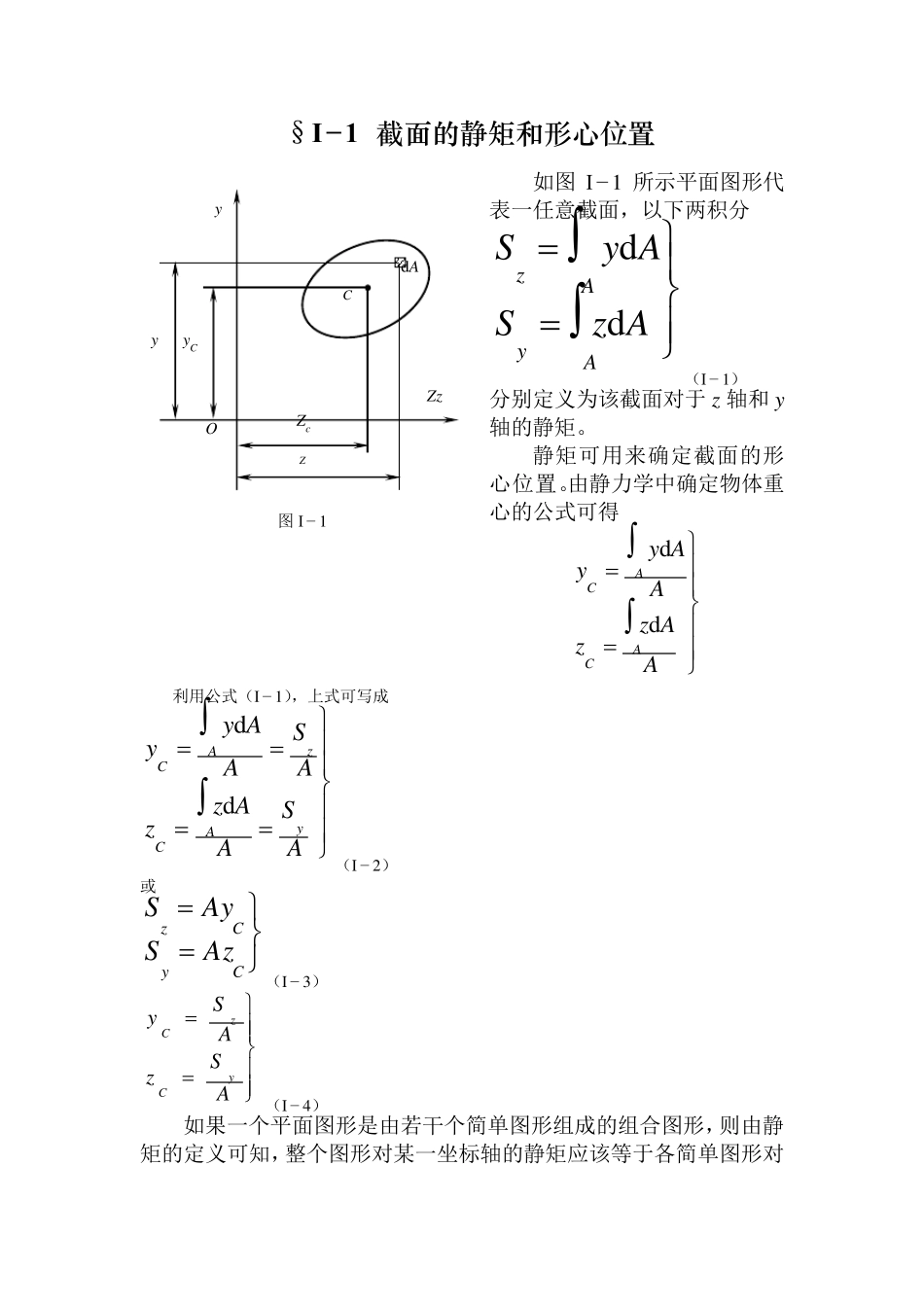
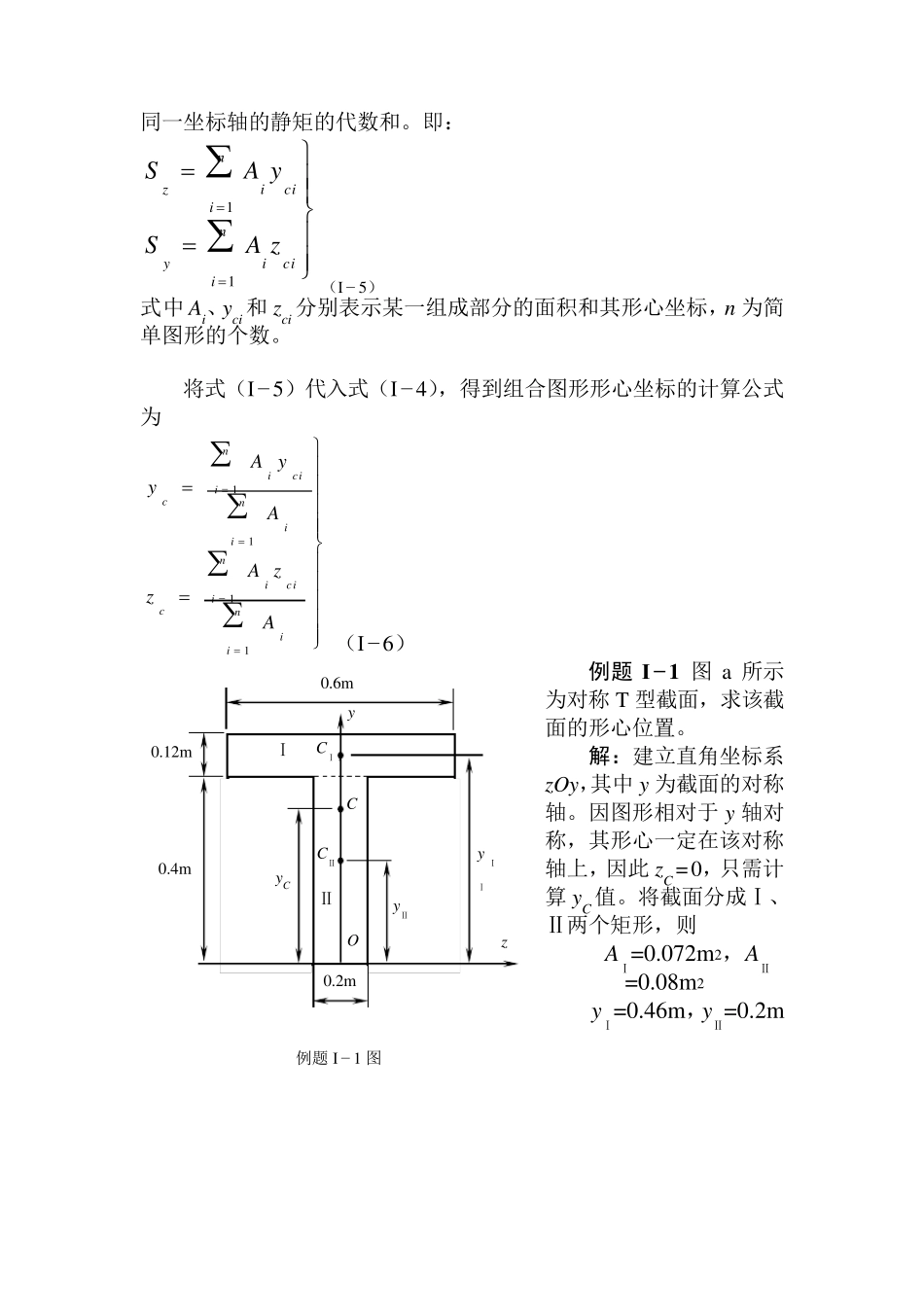
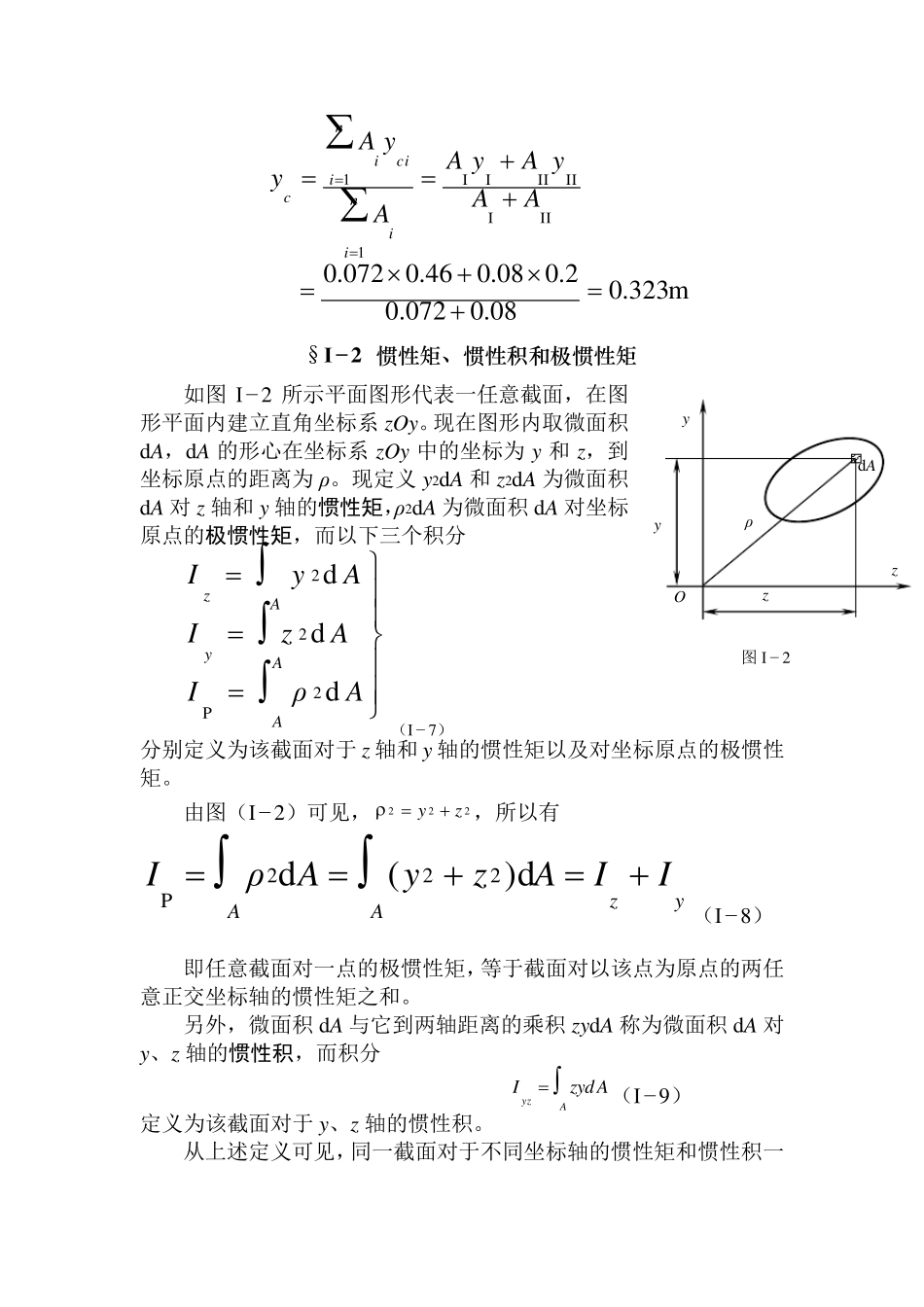
§I− 1 截面的静矩和形心位置 如图 I− 1 所示平面图形代表一任意截面,以下两积分 AzSAySAyAzdd(I − 1 ) 分别定义为该截面对于 z 轴和 y轴的静矩。 静矩可用来确定截面的形心位置。由静力学中确定物体重心的公式可得 AAzzAAyyACACdd 利用公式(I − 1 ),上式可写成 ASAAzzASAAyyyACzACdd(I − 2 ) 或 CyCzAzSAyS(I − 3 ) ASzASyyCzC(I − 4 ) 如果一个平面图形是由若干个简单图形组成的组合图形,则由静矩的定义可知,整个图形对某一坐标轴的静矩应该等于各简单图形对d A C Zz y y yC Zc O 图 I − 1 Z 同一坐标轴的静矩的代数和。即: niciiyniciizzASyAS11(I − 5) 式中Ai、yci 和zci 分别表示某一组成部分的面积和其形心坐标,n 为简单图形的个数。 将式(I− 5)代入式(I− 4),得到组合图形形心坐标的计算公式为 niiniciicniiniciicAzAzAyAy1111(I− 6) 例题 I− 1 图a 所示为对称T 型截面,求该截面的形心位置。 解:建立直角坐标系zOy,其中y 为截面的对称轴。因图形相对于y 轴对称,其形心一定在该对称轴上,因此zC=0,只需计算yC 值。将截面分成Ⅰ、Ⅱ两个矩形,则 AⅠ=0.072m 2,AⅡ=0.08m 2 yⅠ=0.46m ,yⅡ=0.2m yC 0.12m 0.4m yⅡ yⅠⅠ 0.6m 0.2m O y z Ⅰ Ⅱ CⅠⅠ CⅡ C 例题 I − 1 图 m323.008.0072.02.008.046.0072.0IIIIIIIII11 AAyAyAAyAyniiniciic §I− 2 惯性矩、惯性积和极惯性矩 如图 I− 2 所示平面图形代表一任意截面,在图形平面内建立直角坐标系 zOy。现在图形内取微面积dA,dA 的形心在坐标系 zOy 中的坐标为 y 和 z,到坐标原点的距离为 ρ。现定义 y2dA 和 z2dA 为微面积dA 对 z 轴和 y 轴的惯性矩,ρ2dA 为微面积 dA 对坐标原点的极惯性矩,而以下三个积分 AρIAzIAyIAAyAzddd2P22(I − 7) 分别定义为该截面对于 z 轴和 y 轴的惯性矩以及对坐标原点的极惯性矩。 由图(I− 2)可见,222zy ,所以有 AyzAIIAzyAρI)d(d222P(I− 8) 即任意截面对一点的极惯性矩,等于截面对以该点...