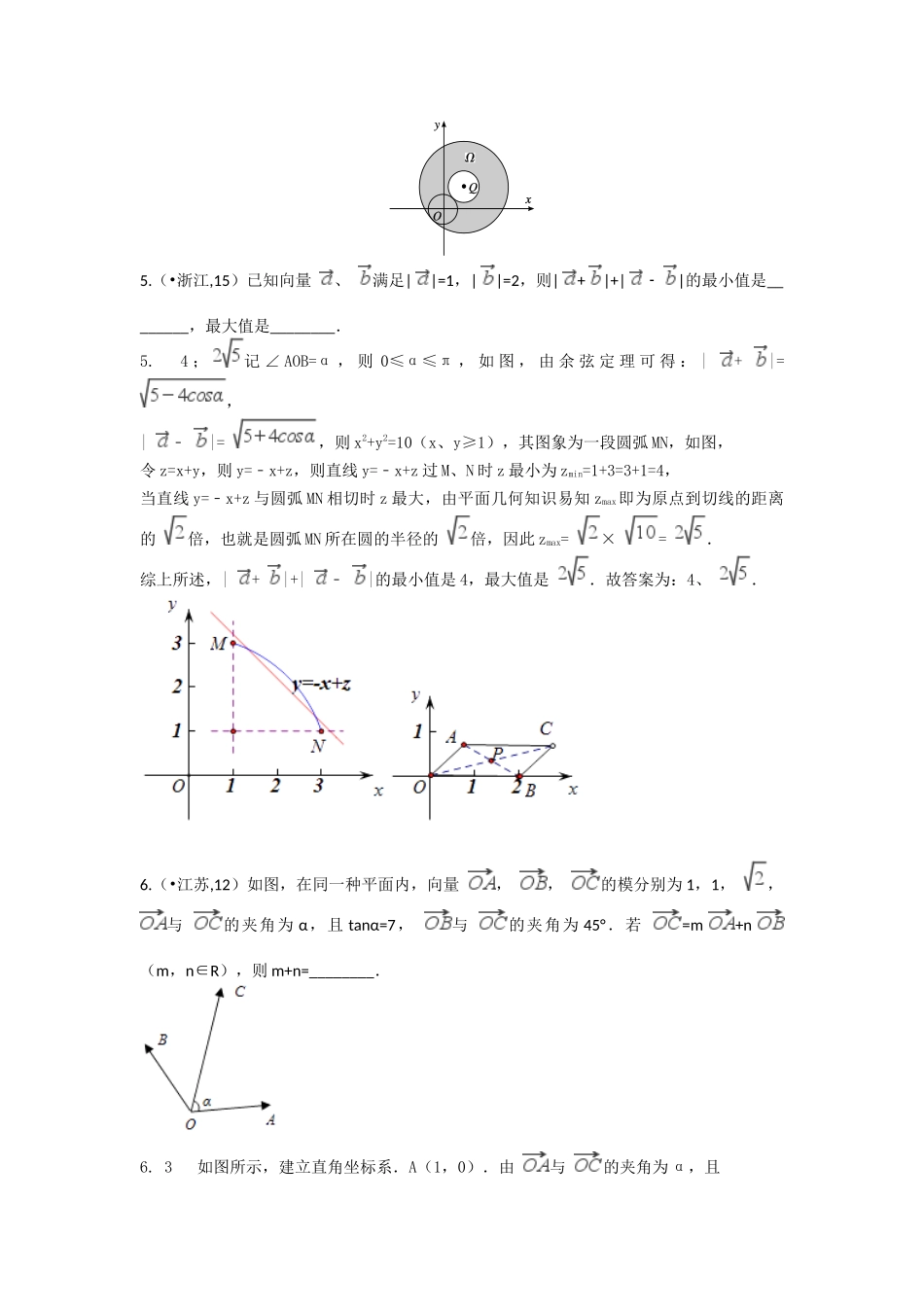
第五章 平面向量考点 1 平面向量的概念及坐标运算1.(·新课标全国Ⅰ,7)设 D 为△ABC 所在平面内一点,BC=3CD,则( )A.AD=-AB+AC B.AD=AB-AC C.AD=AB+AC D.AD=AB-AC1.A[ BC=3CD,∴AC-AB=3(AD-AC),即 4AC-AB=3AD,∴AD=-AB+AC.]2.(·湖南,8)已知点 A,B,C 在圆 x2+y2=1 上运动,且 AB⊥BC.若点 P 的坐标为(2,0),则|PA+PB+PC|的最大值为( )A.6 B.7 C.8 D.92.B [由 A,B,C 在圆 x2+y2=1 上,且 AB⊥BC,∴AC 为圆直径,故PA+PC=2PO=(-4,0),设 B(x,y),则 x2+y2=1 且 x∈[-1,1],PB=(x-2,y),因此PA+PB+PC=(x-6,y).故|PA+PB+PC|=,∴x=-1 时有最大值=7,故选 B.]3.(·福建,8)在下列向量组中,可以把向量 a=(3,2)表达出来的是( )A.e1=(0,0),e2=(1,2) B.e1=(-1,2),e2=(5,-2)C.e1=(3,5),e2=(6,10) D.e1=(2,-3),e2=(-2,3)3.B [法一 若 e1=(0,0),e2=(1,2),则 e1∥e2,而 a 不能由 e1,e2表达,排除 A;若 e1=(-1,2),e2=(5,-2),由于≠,因此 e1,e2不共线,根据共面向量的基本定理,可以把向量 a=(3,2)表达出来,故选 B.法二 由于 a=(3,2),若 e1=(0,0),e2=(1,2),不存在实数 λ,μ,使得 a=λe1+μe2,排除 A;若 e1=(-1,2),e2=(5,-2),设存在实数 λ,μ,使得 a=λe1+μe2,则(3,2)=(-λ+5μ,2λ-2μ),因此解得因此 a=2e1+e2,故选 B.]4.(·安徽,10)在平面直角坐标系 xOy 中,已知向量 a,b,|a|=|b|=1,a·b=0,点 Q 满足OQ=(a+b).曲线 C={P|OP=acosθ+bcosθ,0≤θ<2π},区域 Ω={P|0