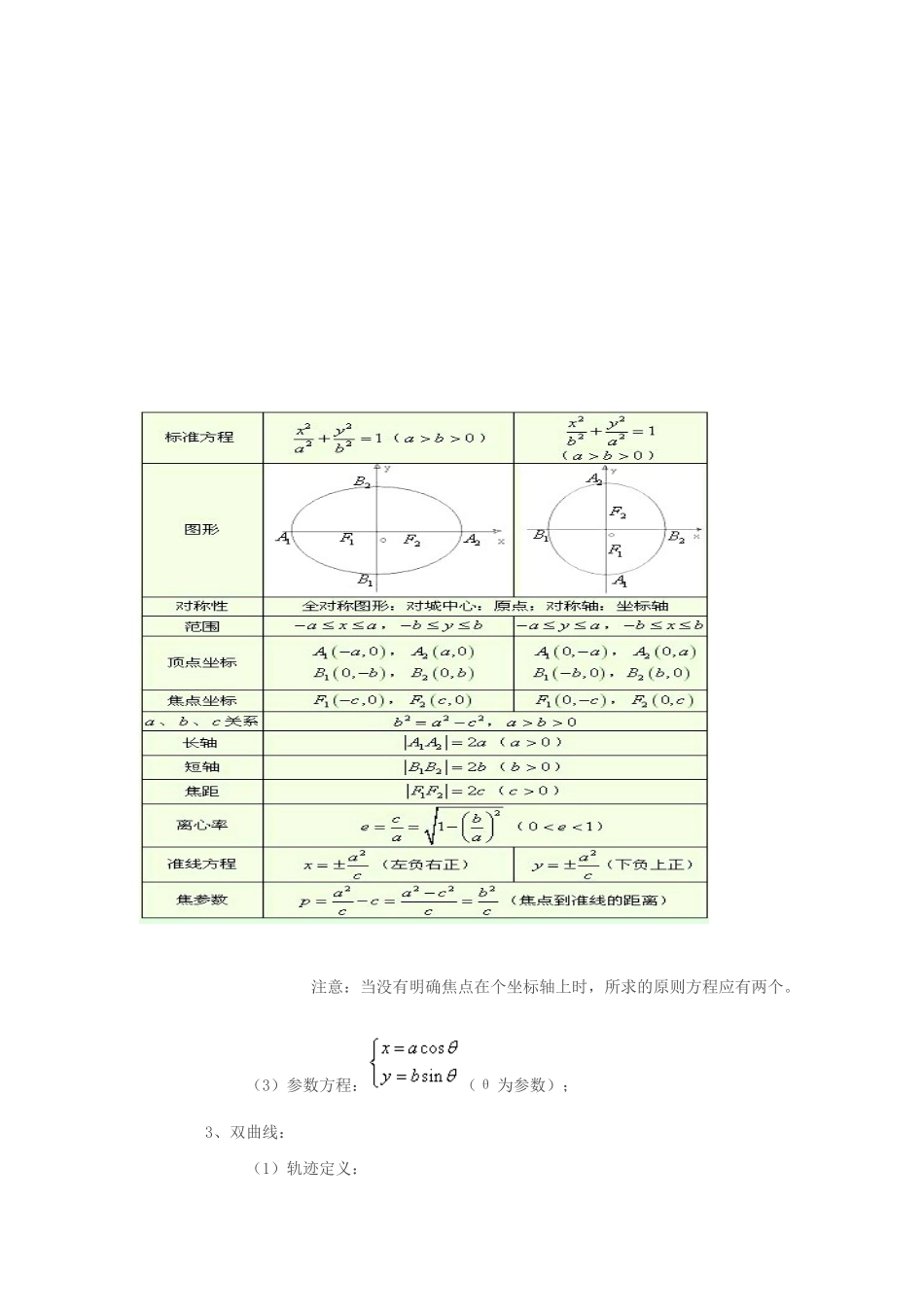
高中数学知识点大全—圆锥曲线一、考点(限考)概要: 1、椭圆: (1)轨迹定义: ① 定义一:在平面内到两定点的距离之和等于定长的点的轨迹是椭圆,两定点是焦点,两定点间距离是焦距,且定长 2a 不小于焦距 2c。用集合表达为:; ② 定义二:在平面内到定点的距离和它到一条定直线的距离之比是个常数 e,那么这个点的轨迹叫做椭圆。其中定点叫焦点,定直线叫准线,常数是离心率 用集合表达为:; (2)原则方程和性质: 注意:当没有明确焦点在个坐标轴上时,所求的原则方程应有两个。 (3)参数方程:(θ 为参数); 3、双曲线: (1)轨迹定义: ① 定义一:在平面内到两定点的距离之差的绝对值等于定长的点的轨迹是双曲线,两定点是焦点,两定点间距离是焦距。用集合表达为: ② 定义二:到定点的距离和它到一条定直线的距离之比是个常数 e,那么这个点的轨迹叫做双曲线。其中定点叫焦点,定直线叫准线,常数 e 是离心率。 用集合表达为: (2)原则方程和性质: 注意:当没有明确焦点在个坐标轴上时,所求的原则方程应有两个。 4、抛物线: (1)轨迹定义:在平面内到定点和定直线的距离相等的点的轨迹是抛物线,定点是焦点,定直线是准线,定点与定直线间的距离叫焦参数 p。用集合表达为: (2)原则方程和性质: ① 焦点坐标的符号与方程符号一致,与准线方程的符号相反; ②原则方程中一次项的字母与对称轴和准线方程的字母一致;③ 原则方程的顶点在原点,对称轴是坐标轴,有别于一元二次函数的图像;二、复习点睛: 1、平面解析几何的知识构造: 2、椭圆各参数间的关系请记熟 “六点六线,一种三角形”,即六点:四个顶点,两个焦点;六线:两条准线,长轴短轴,焦点线和垂线 PQ;三角形:焦点三角形。则椭圆的各性质(除切线外)均可在这个图中找到。 3、椭圆形状与 e 的关系:当 e→0,c→0,椭圆→圆,直至成为极限位置的圆,则认为圆是椭圆在 e=0 时的特例。当 e→1,c→a 椭圆变扁,直至成为极限位置的线段,此时也可认为是椭圆在 e=1 时的特例。 4、运用焦半径公式计算焦点弦长:若斜率为 k 的直线被圆锥曲线所截得的弦为AB,A、B 两点的坐标分别为,则弦长 这里体现理解析几何“设而不求”的解题思想。 5、若过椭圆左(或右)焦点的焦点弦为 AB,则; 6、结合下图熟记双曲线的:“四点八线,一种三角形”,即:四点:顶点和焦点;八线:实轴、虚轴、准线、渐进线、焦...