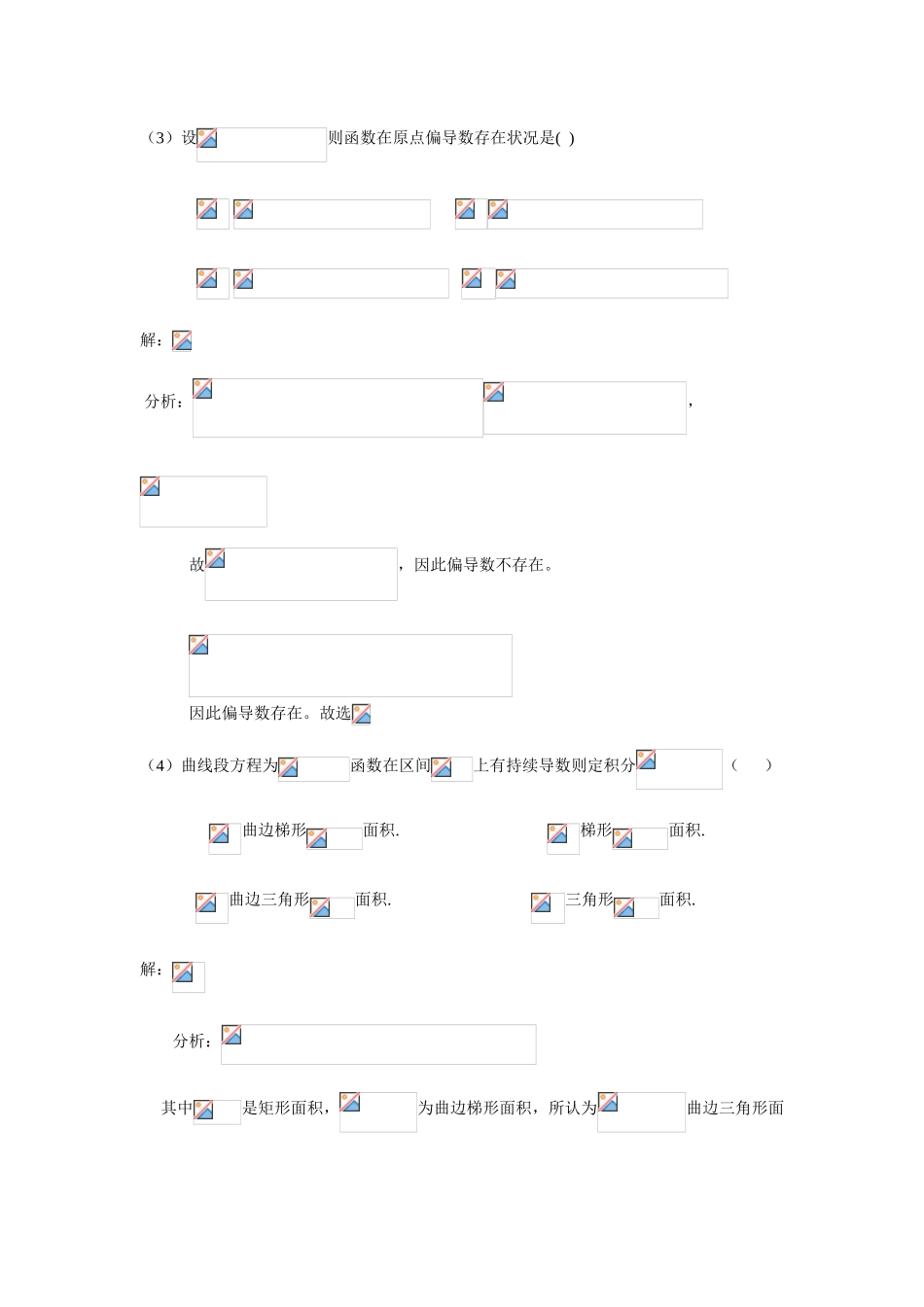
全国硕士硕士入学统一考试数学三试题详解一、选择题:1~8 小题,每题 4 分,共 32 分,下列每题给出四个选项中,只有一项符合题目规定,把所选项前字母填在题后括号内.(1)设函数在区间上持续,则是函数( )跳跃间断点. 可去间断点.无穷间断点. 振荡间断点.解:分析:,因此是函数可去间断点。(2)设持续,,,,则,则( ) 解:选分析;用极坐标得(3)设则函数在原点偏导数存在状况是( ) 解: 分析:,故,因此偏导数不存在。因此偏导数存在。故选(4)曲线段方程为函数在区间上有持续导数则定积分( )曲边梯形面积. 梯形面积.曲边三角形面积.三角形面积.解:分析: 其中是矩形面积,为曲边梯形面积,所认为曲边三角形面积。(5)设为阶非 0 矩阵为阶单位矩阵若,则( )不可逆,不可逆.不可逆,可逆.可逆,可逆. 可逆,不可逆. 解:分析:,故均可逆。(6)设则在实数域上和协议矩阵为( )... . 解:分析:则。记,则则正、负惯性指数相似,故选(7)随机变量独立同分布且分布函数为,则分布函数为( ) . . . . 解:分析:(8)随机变量,且有关系数,则( ) .... 解:选 分析: 用排除法设,由,懂得正有关,得,排除、由,得排除 故选择二、填空题:9-14 小题,每题 4 分,共 24 分,请将答案写在答题纸指定位置上.(9)设函数在内持续,则 . 解:1分析:由(10)函数,求积分 .解:分析:因此(11).其中解:分析:(12)微分方程求方程特解.解:分析:由因此,又,因此.(13)设 3 阶矩阵特性值 1,2,2, .解:特性值为 1,2,2,则存在可逆矩阵,使得分析:,因,则(14)设随机变量服从参数为 1 泊松分布,则.解:分析:由于 ,因此 ,服从参数为 1 泊松分布,因此 三、解答题:15-23 小题,共 94 分.请将解答写在答题纸指定位置上.解答应写出文字阐明、证明过程或演算环节.(15) (本题满分 10 分)求极限.解: (16) (本题满分 10 分) 设是由方程所确定函数,其中具有 2 阶导数且时,求(1)(2)记,求.解:①②(17) (本题满分 10 分)是周期为 2 持续函数,(1)证明对任意实数所有有(2)证明是周期为 2 周期函数.解:(1)对于,令,则由于周期为 2,因此因此(2)由于因此因此因此是周期为 2 周期函数(18) (本题满分 10 分)求二重积分其中解: (19) (本题满分 10 分)已知年复利为 0.05,现存万元,第一年取出 19 万元,...