材料力学第五版课后习题答案

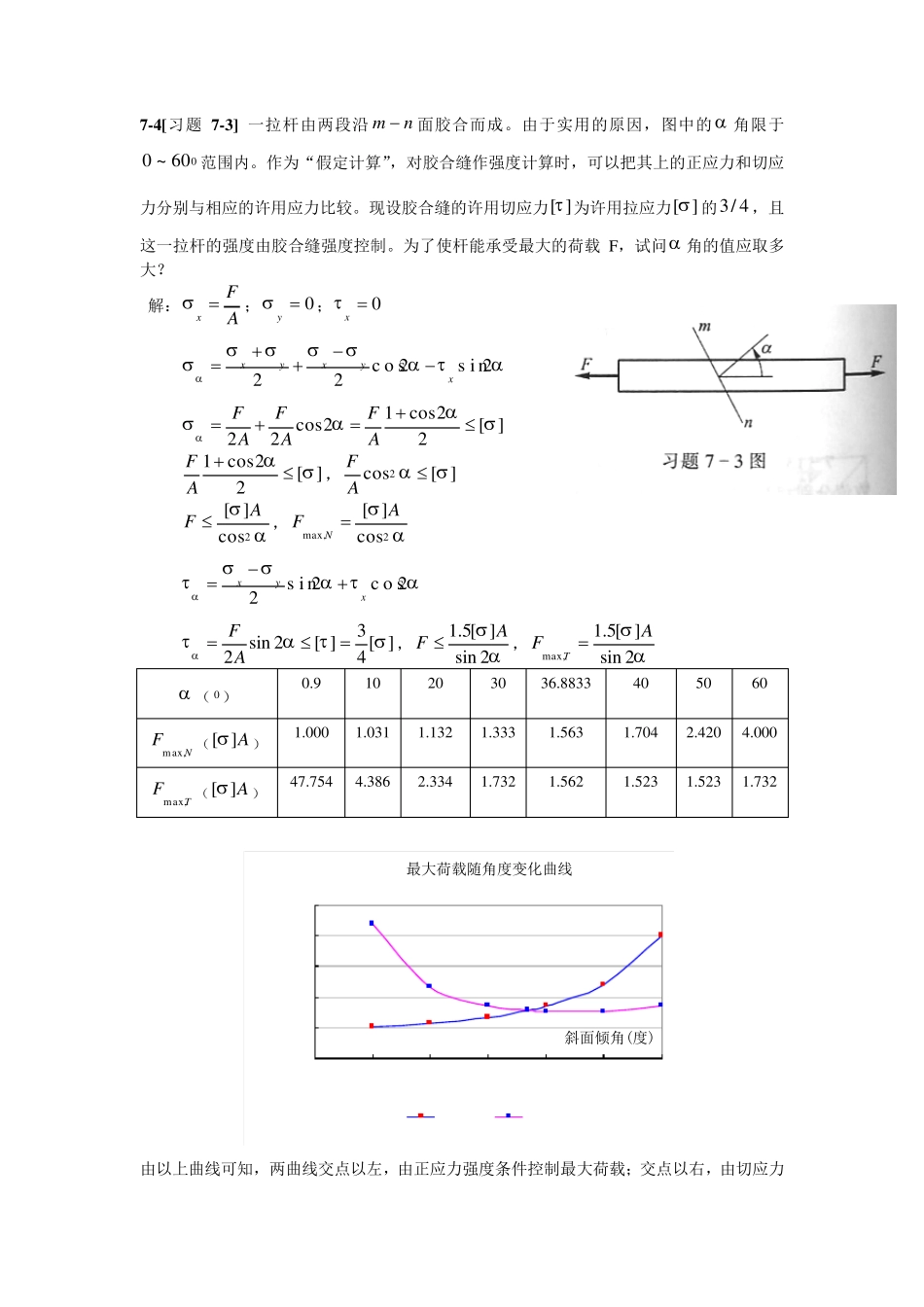
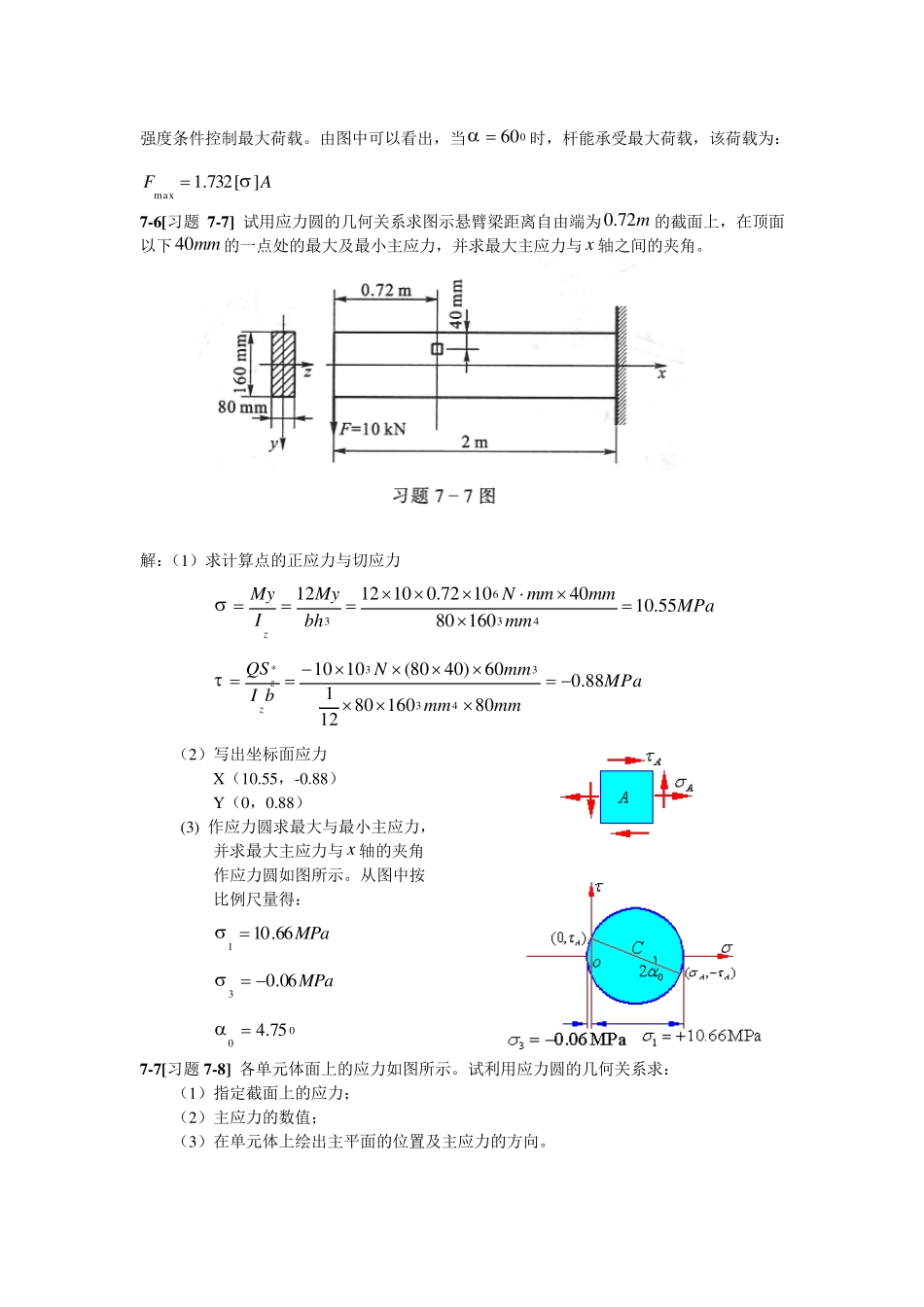
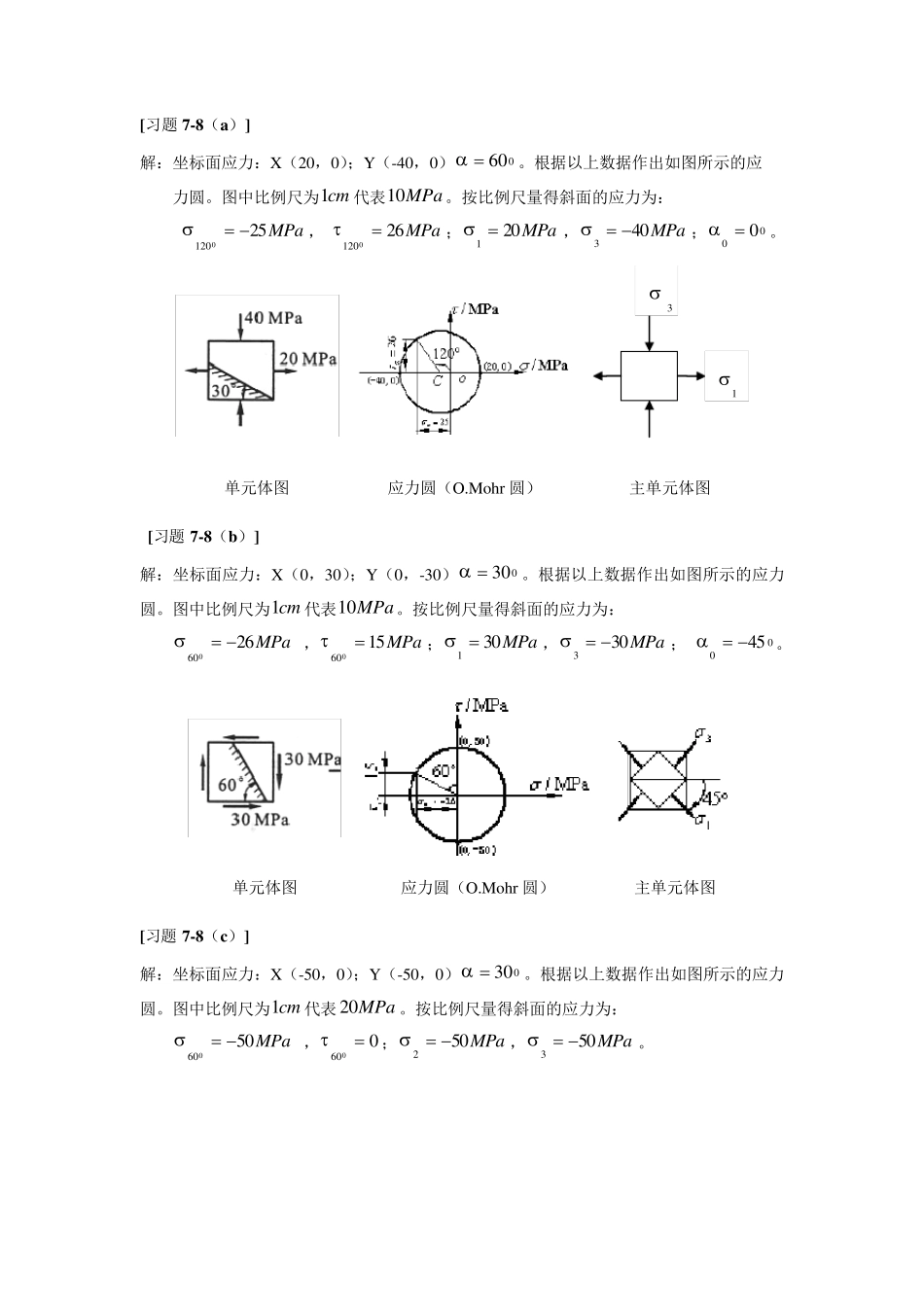
7-4[习题7-3] 一拉杆由两段沿nm 面胶合而成。由于实用的原因，图中的 角限于060~0范围内。作为“假定计算”，对胶合缝作强度计算时，可以把其上的正应力和切应力分别与相应的许用应力比较。现设胶合缝的许用切应力][ 为许用拉应力][ 的4/3，且这一拉杆的强度由胶合缝强度控制。为了使杆能承受最大的荷载 F，试问 角的值应取多大？ 解：AFx ；0y；0x 2s i n2c o s22xyxyx ][22cos12cos22AFAFAF ][22cos1 AF，][cos2 AF 2cos][AF ，2max,cos][AFN  2c o s2s i n2xyx ][43][2sin2AF，2sin][5.1AF ，2sin][5.1max,AFT   （ 0 ） 0.9 10 20 30 36.8833 40 50 60 NFmax, （A][） 1.000 1.031 1.132 1.333 1.563 1.704 2.420 4.000 TFmax, （A][） 47.754 4.386 2.334 1.732 1.562 1.523 1.523 1.732 最大荷载随角度变化曲线0.0001.0002.0003.0004.0005.0000102030405060斜面倾角(度)Fmax,N,Fmax,TFmax,NFmax,T 由以上曲线可知，两曲线交点以左，由正应力强度条件控制最大荷载；交点以右，由切应力强度条件控制最大荷载。由图中可以看出，当060时，杆能承受最大荷载，该荷载为： AF][732.1max 7-6[习题 7-7] 试用应力圆的几何关系求图示悬臂梁距离自由端为m72.0的截面上，在顶面以下mm40的一点处的最大及最小主应力，并求最大主应力与 x 轴之间的夹角。 解：（1）求计算点的正应力与切应力 MPammmmmmNbhMyIMyz55.1016080401072.01012124363 MPammmmmmNbIQSzz88.0801608012160)4080(10104333* （2）写出坐标面应力 X（10.55，-0.88） Y（0，0.88） (3) 作应力圆求最大与最小主应力， 并求最大主应力与 x 轴的夹角 作应力圆如图所示。从图中按 比例尺量得： MPa66.101  MPa06.03 0075.4 7-7[习题 7-8] 各单元体面上的应力如图所示。试利用应力圆的几何关系求： （1）指定截面上的应力； （2）主应力的数值； （3）在单元体上绘出主平面的位置及主应力的方向。 [习题7-8（a）] 解：坐标面应力：X（20，0）；Y（-40，0） 060。根据以上数据作出如图所示的应 力圆。图中比例尺为 cm1代表MPa10。按比例尺量得斜面的应...