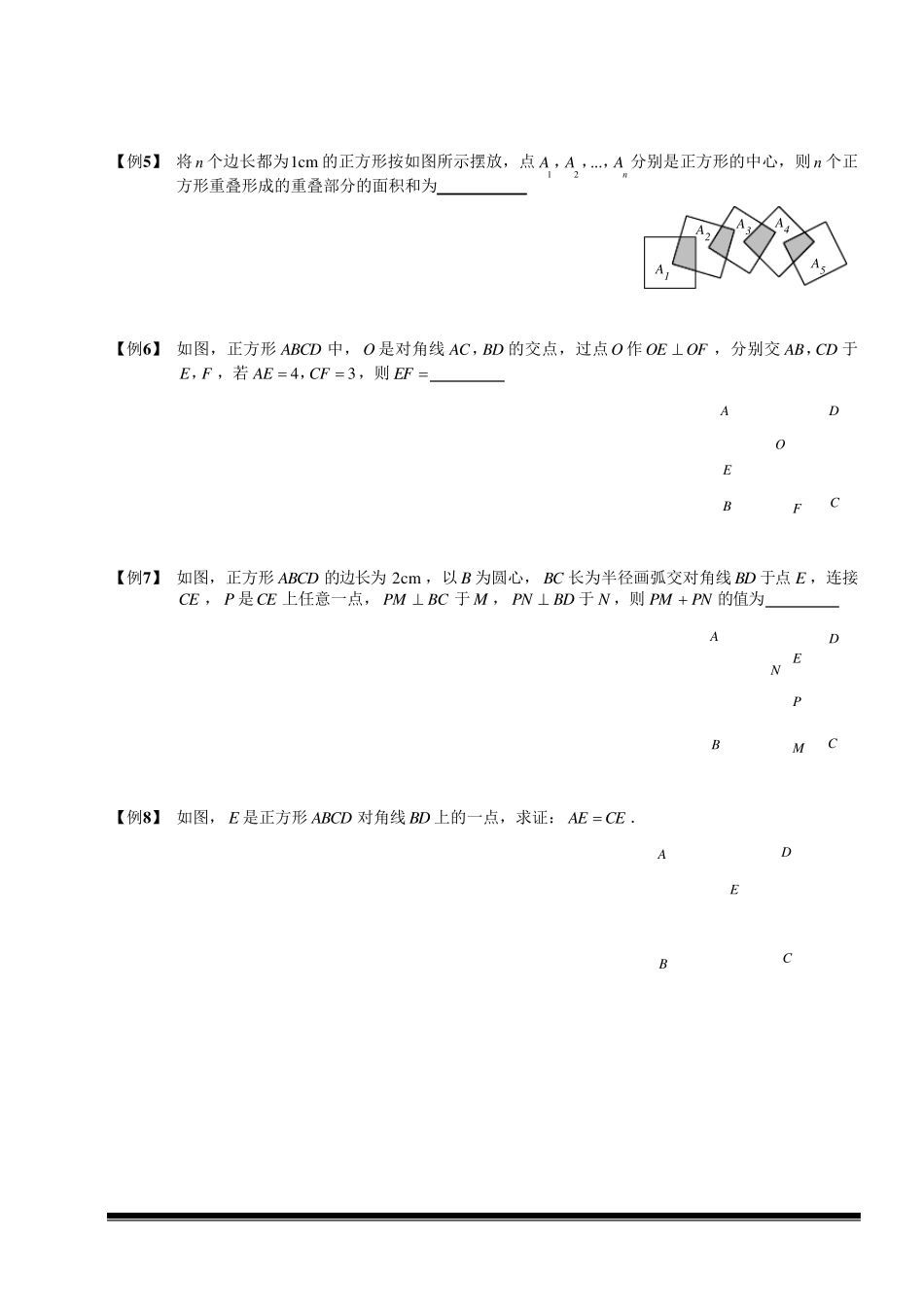
1.正方形的定义:有 一 组 邻 边 相 等 , 并 且 有 一 个 角 是 直 角 的 平 行 四 边 形 叫 做 正 方 形 . 2.正方形的性质 正 方 形 是 特 殊 的 平 行 四 边 形 、矩形 、菱形 . 它具有 前三者的 所有 性质: ① 边 的 性质:对边 平 行 , 四 条边 都相 等 . ② 角 的 性质:四 个 角 都是 直 角 . ③ 对角 线性质:两条对角 线互相 垂直 平 分且 相 等 , • 每条对角 线平 分一 组 对角 . ④ 对称性:正 方 形 是 中心对称图形 , 也是 轴对称图形 . 平 行 四 边 形 、矩形 、菱形 和正 方 形 的 关系:(如图) 3.正方形的判定 判定①:有 一 组 邻 边 相 等 的 矩形 是 正 方 形 . 判定②:有 一 个 角 是 直 角 的 菱形 是 正 方 形 . 一、正方形的性质 【例1】 正方形有 条对称轴. 【例2】 已知正方形BDEF 的边长是正方形ABCD 的对角线,则:BDEFABCDSS正方形正方形 【例3】 如图,已知正方形ABCD 的面积为 256 ,点 F 在CD 上,点 E 在CB 的延长线上,且 20AEAFAF,,则 BE 的长为 FEDCBA 【例4】 如图,在正方形ABCD 中, E 为 AB 边的中点, G , F 分别为 AD , BC 边上的点,若1AG ,2BF ,90GEF,则 GF 的长为 . 正方形的性质 及判定 正方形菱形矩形平行四边形 【例5】 将 n个边长都为1cm 的正方形按如图所示摆放,点12 ...nAAA, , , 分别是正方形的中心,则 n个正方形重叠形成的重叠部分的面积和为 A5A4A3A2A1 【例6】 如图,正方形 ABCD 中, O 是对角线 AC BD,的交点,过点 O 作 OEOF,分别交 AB CD,于E F, ,若43AECF,,则 EF OFEDCBA 【例7】 如图,正方形 ABCD 的边长为 2cm ,以 B 为圆心, BC 长为半径画弧交对角线 BD 于点 E ,连接CE , P 是CE 上任意一点, PMBC于 M , PNBD于 N ,则 PMPN的值为 PNMEDCBA 【例8】 如图, E 是正方形 ABCD 对角线 BD 上的一点,求证: AECE. EDCBA 【例9】 如图,P为正方形ABCD 对角线上一点,PEBC于E ,PFCD于F .求证:APEF. FEPDCBA 【例10】 如图所示,正方形ABCD 对角线AC 与BD 相交于O ,MN ∥ AB ,且分别与AOBO、交于MN、.试探...