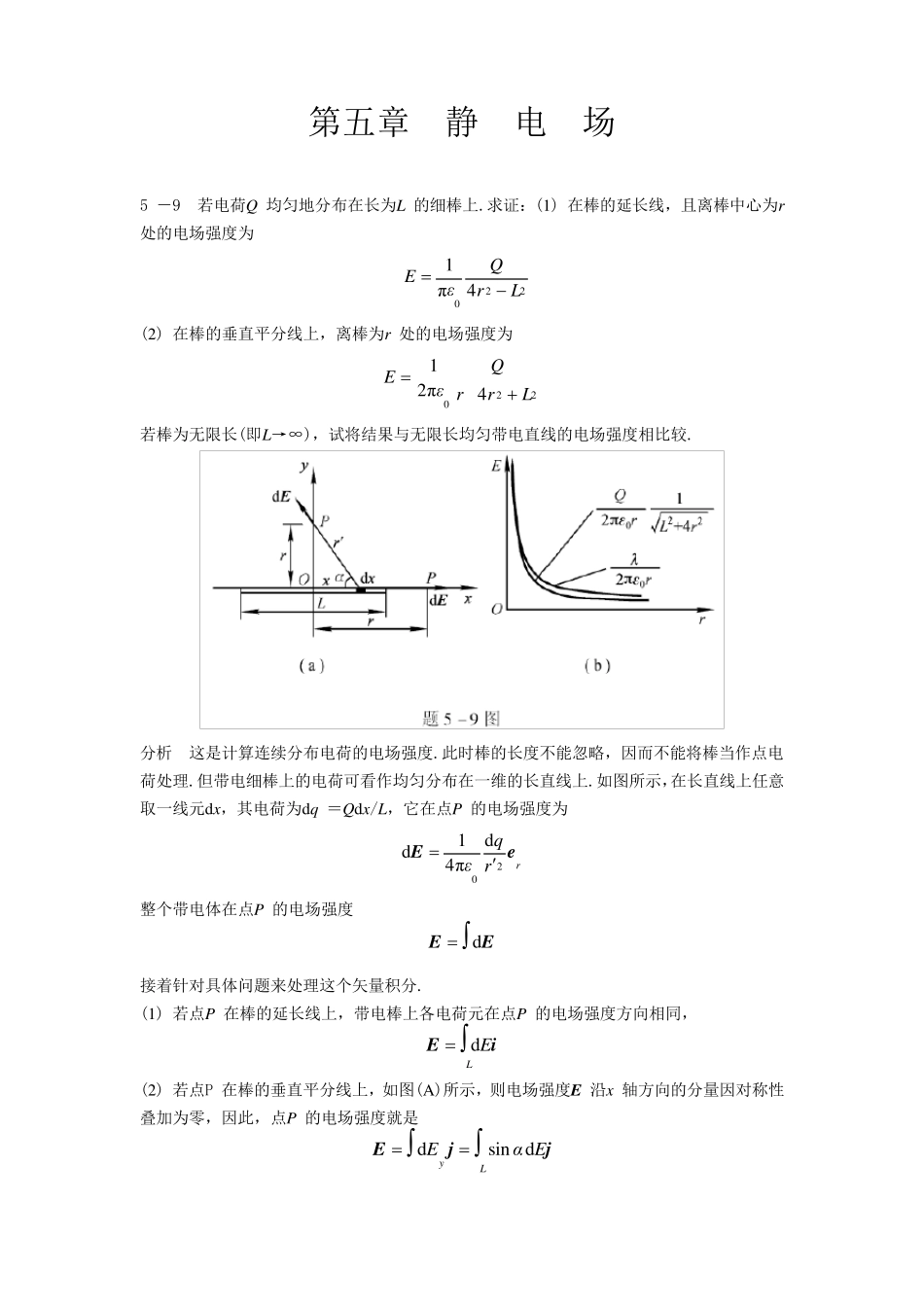
第五章 静 电 场 5 -9 若电荷Q 均匀地分布在长为L 的细棒上.求证:(1) 在棒的延长线,且离棒中心为r 处的电场强度为 220 4π1LrQεE (2) 在棒的垂直平分线上,离棒为r 处的电场强度为 2204π21LrrQεE 若棒为无限长(即L→∞),试将结果与无限长均匀带电直线的电场强度相比较. 分析 这是计算连续分布电荷的电场强度.此时棒的长度不能忽略,因而不能将棒当作点电荷处理.但带电细棒上的电荷可看作均匀分布在一维的长直线上.如图所示,在长直线上任意取一线元dx,其电荷为dq =Qdx/L,它在点P 的电场强度为 rrqεeE20dπ41d 整个带电体在点P 的电场强度 EEd 接着针对具体问题来处理这个矢量积分. (1) 若点P 在棒的延长线上,带电棒上各电荷元在点P 的电场强度方向相同, LEiEd (2) 若点P 在棒的垂直平分线上,如图(A)所示,则电场强度E 沿x 轴方向的分量因对称性叠加为零,因此,点P 的电场强度就是 LyEαEjjEdsind 证 (1) 延长线上一点P 的电场强度LrπεqE202d,利用几何关系 r′=r -x统一积分变量,则 220022204π12/12/1π4dπ41LrQεLrLrLεQxrLxQεEL/-L/P 电场强度的方向沿x 轴. (2) 根据以上分析,中垂线上一点P 的电场强度E 的方向沿y 轴,大小为 ErεqαELdπ4dsin20 利用几何关系 sin α=r/r′,22xrr 统一积分变量,则 2203/22222041π2dπ41LrrεQrxLxrQεEL/-L/ 当棒长L→∞时,若棒单位长度所带电荷λ为常量,则P 点电场强度 rελLrLQrεEl0220π2 /41/π21lim 此结果与无限长带电直线周围的电场强度分布相同[图(B)].这说明只要满足r2/L2 <<1,带电长直细棒可视为无限长带电直线. 5 -14 设匀强电场的电场强度E 与半径为R 的半球面的对称轴平行,试计算通过此半球面的电场强度通量. 分析 方法1:由电场强度通量的定义,对半球面S 求积分,即SSdsEΦ 方法2:作半径为R 的平面S′与半球面S 一起可构成闭合曲面,由于闭合面内无电荷,由高斯定理 01d0qεSSE 这表明穿过闭合曲面的净通量为零,穿入平面S′的电场强度通量在数值上等于穿出半球面S 的电场强度通量.因而 SSSESEΦdd 解1 由于闭合曲面内无电荷分布,根据高斯定理,有 SSSESEΦdd 依照约定取闭合曲面的外法线方向为...