电路理论基础课后习题答案陈希有主编第十到十四章

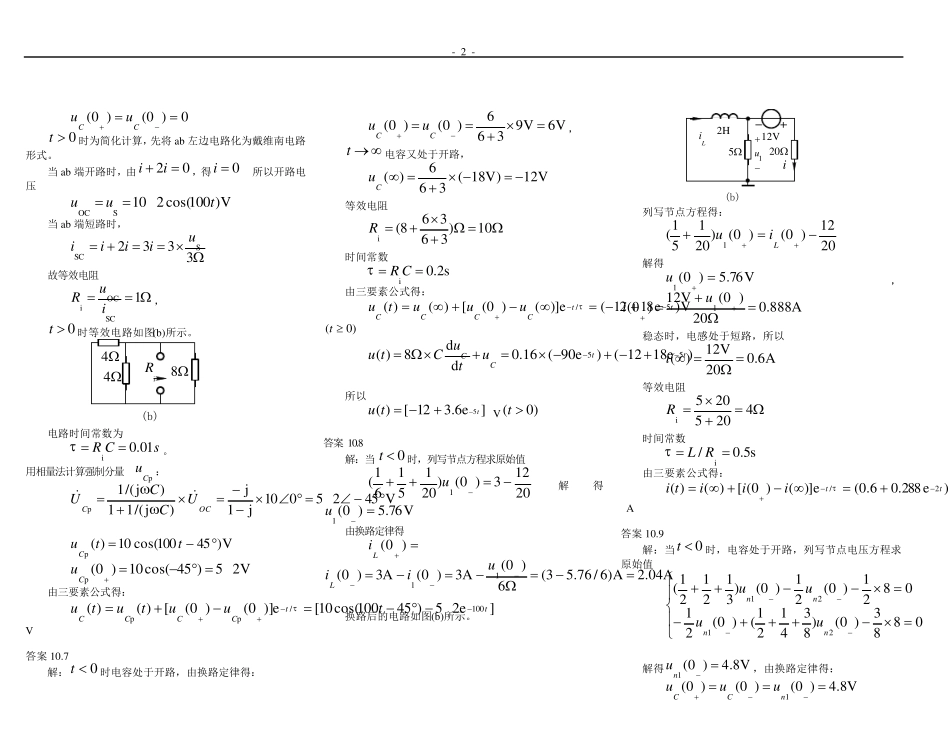
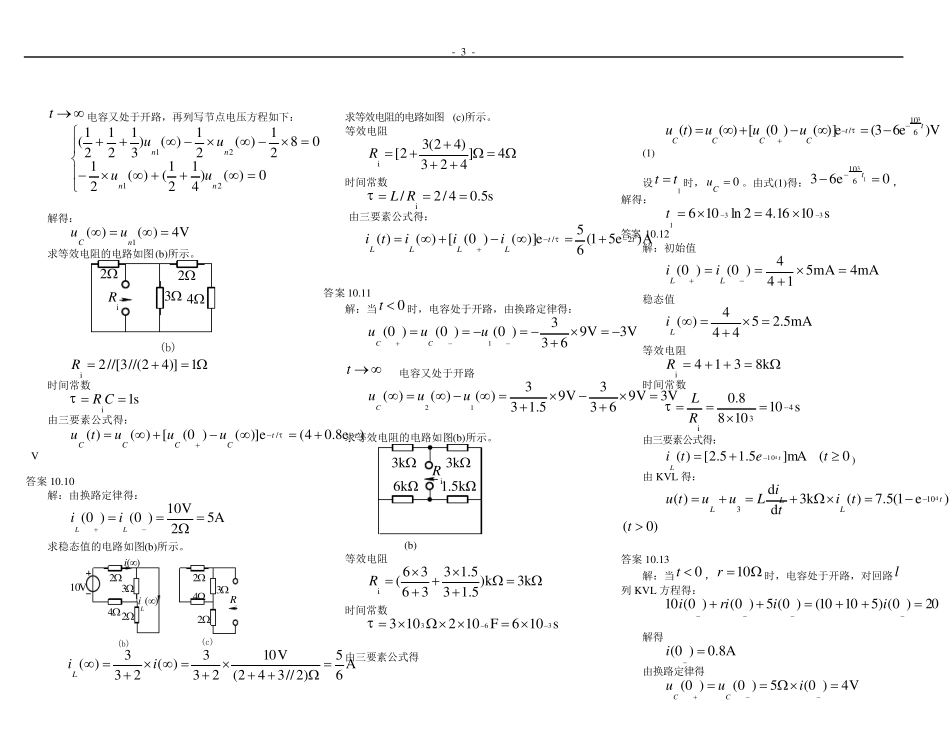
- 1 - 答案10.1 解：0t时，电容处于开路，故 V20k2mA10)0(Cu 由换路定律得： V20)0()0(CCuu 换路后一瞬间，两电阻为串联，总电压为)0(Cu。 所以 mA5k)22()0()0(1Cui 再由节点①的 KCL 方程得： mA5mA)510()0(mA10)0(1iiC 答案10.2 解：0t时电容处于开路，电感处于短路，3电阻与 6电阻相并联，所以 A3)363685(V45)0(i ，A2)0(366)0(iiL V24)0(8)0(iuC 由换路定律得： V24)0()0(CCuu，A2)0()0(LLii 由KVL 得开关电压： V8V)2824()0(8)0()0(LCiuu 答案10.3 解：0t时电容处于开路，0i，受控源源电压04 i，所以 V6.0V5.1)69(6)0()0()0(1uuuCC 0t时，求等效电阻的电路如图(b)所示。 ii436ui(b) 等效电阻 5)36(4iiiiiuR 时间常数 s1.0iCR 0t后电路为零输入响应，故电容电压为： Ve6.0e)0()(10/ttCCutu 6电阻电压为： Ve72.0)dd(66)(101tCtuCitu)0( t 答案10.4 解：0t时电感处于短路，故A3A9363)0(Li，由换路定律得： A3)0()0(LLii 求等效电阻的电路如图(b)所示。 (b)663iR 等 效 电阻836366iR，时间常 数s5.0/i RL 0t后电路为零输入响应，故电感电流为 Ae3e)0()(2/ttLLiti)0( t 电感电压 Ve24dd)(21tLtiLtu)0( t 3电阻电流为 Ae23632133tLuiui 3电阻消耗的能量为： W3]e25.0[1212304040233ttdtedtiW 答案10.5 解：由换路定律得0)0()0(LLii，达到稳态时电感处于短路，故 A54/20)(Li 求等效电阻的电路如图(b)所示。 iR(b)448 等效电阻 6.18//)4//4(iR 时间常数 s)16/1(/i RL 0t后电路为零状态响应，故电感电流为： A)e1(5)e1)(()(16/ttLLiti)0( t Ae8e1651.08/)dd(8)(1616ttLLtiLuti)0( t 答案10.6 解：0t时电路为零状态，由换路定律得： - 2 - 0)0()0(CCuu 0t时为简化计算，先将ab 左边电路化为戴维南电路形式。 当 ab 端开路时，由02  ii，得0i 所以开路电压 V)100cos(210SOCtu...