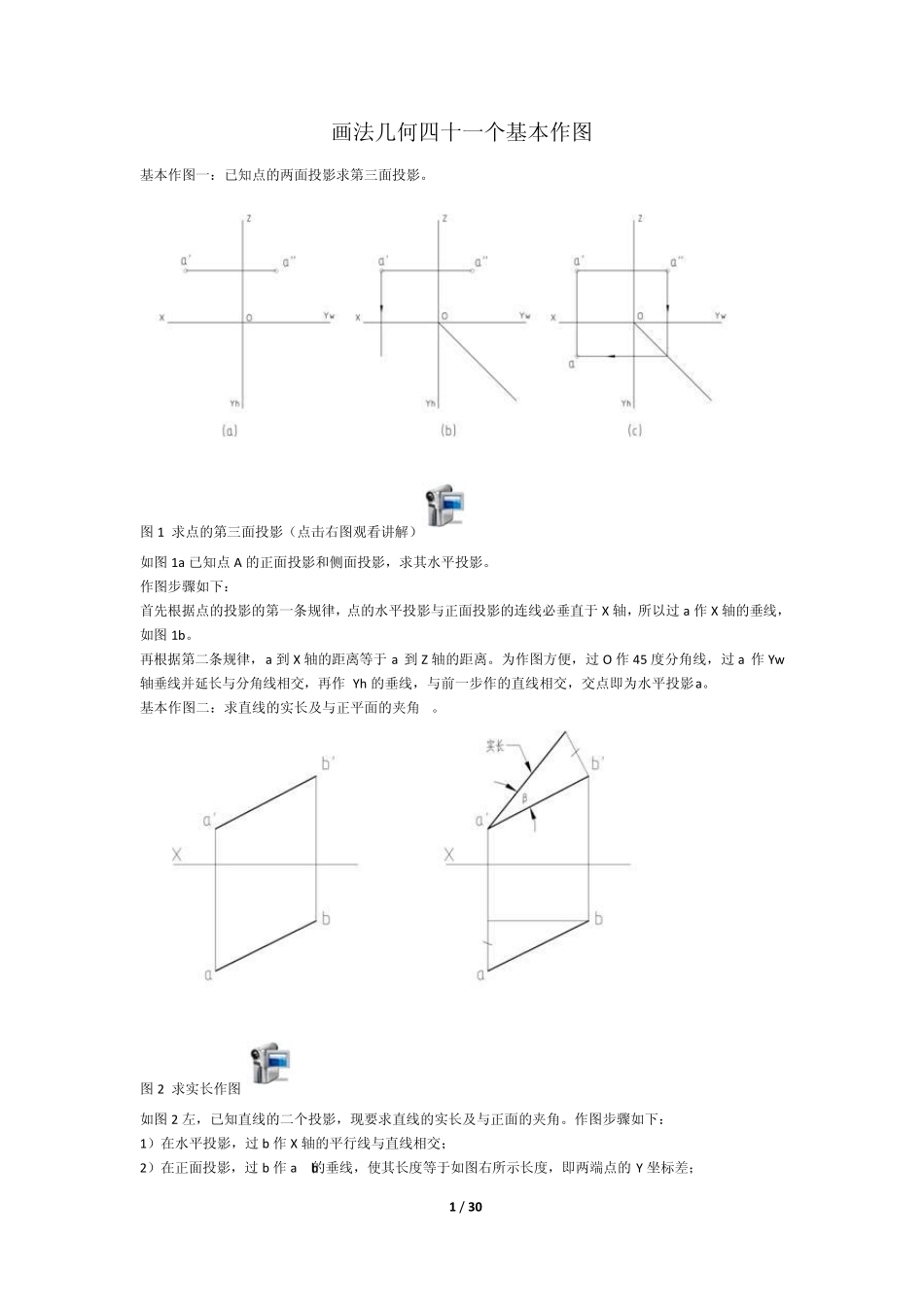
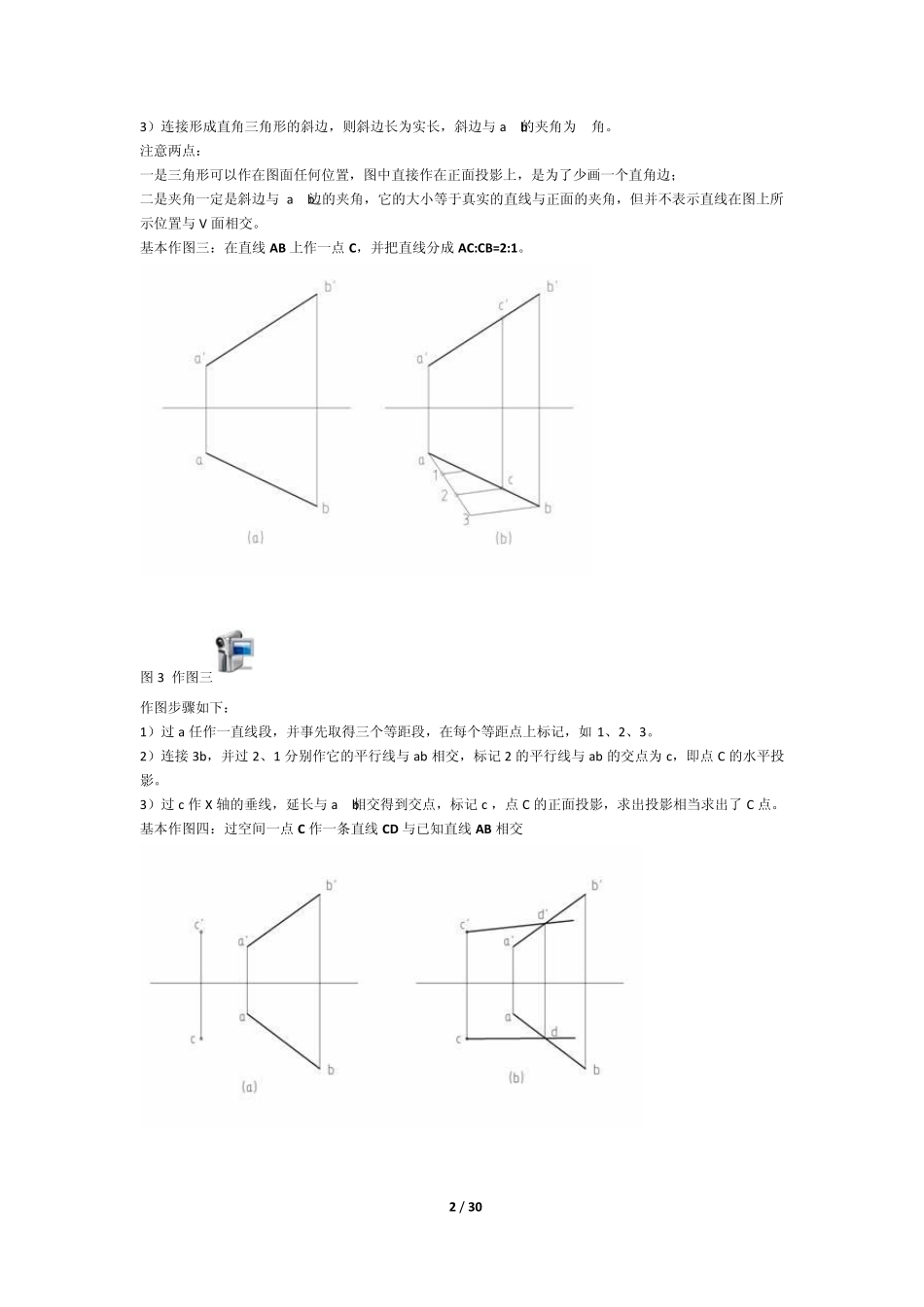
1 / 30 画法几何四十一个基本作图 基本作图一:已知点的两面投影求第三面投影。 图1 求点的第三面投影(点击右图观看讲解) 如图1a 已知点A 的正面投影和侧面投影,求其水平投影。 作图步骤如下: 首先根据点的投影的第一条规律,点的水平投影与正面投影的连线必垂直于 X 轴,所以过 a’作X 轴的垂线,如图1b。 再根据第二条规律,a 到 X 轴的距离等于 a”到 Z 轴的距离。为作图方便,过 O 作45 度分角线,过 a”作Yw轴垂线并延长与分角线相交,再作Yh 的垂线,与前一步作的直线相交,交点即为水平投影a。 基本作图二:求直线的实长及与正平面的夹角 β。 图2 求实长作图 如图2 左,已知直线的二个投影,现要求直线的实长及与正面的夹角。作图步骤如下: 1)在水平投影,过 b 作X 轴的平行线与直线相交; 2)在正面投影,过 b’作a’b’的垂线,使其长度等于如图右所示长度,即两端点的Y 坐标差; 2 / 30 3)连接形成直角三角形的斜边,则斜边长为实长,斜边与a’b’的夹角为β角。 注意两点: 一是三角形可以作在图面任何位置,图中直接作在正面投影上,是为了少画一个直角边; 二是夹角一定是斜边与a’b’边的夹角,它的大小等于真实的直线与正面的夹角,但并不表示直线在图上所示位置与V 面相交。 基本作图三:在直线AB 上作一点C,并把直线分成AC:CB=2:1。 图3 作图三 作图步骤如下: 1)过a 任作一直线段,并事先取得三个等距段,在每个等距点上标记,如1、2、3。 2)连接3b,并过2、1 分别作它的平行线与ab 相交,标记2 的平行线与ab 的交点为c,即点C 的水平投影。 3)过c 作X 轴的垂线,延长与a’b’相交得到交点,标记c’,点C 的正面投影,求出投影相当求出了C 点。 基本作图四:过空间一点C 作一条直线CD 与已知直线AB 相交 3 / 30 图4 过点作直线相交 作图步骤如图4b 所示: 1)由于过一点可作无数条直线与已知直线AB 相交,现在是任作一条。过c’作任一直线c’d’与a’b’ 相交于d’。 2)过d’作投影轴的垂线并延长交ab 于d。 3)连接 cd,并延长。 作直线与直线相交的关键是要保证直线投影的交点,是直线在空间交点的投影。 基本作图五:过点C 作一条直线CD 与已知直线AB 平行 图5 过点作平行 作图步骤如5b 所示: 1)过c’作c’d’平行于a’b’; 2)过c 作cd 平行于ab; 3)使 d’和 d 在一条垂直于投影轴的直线上。这是...