相似的基本模型教师版带答案

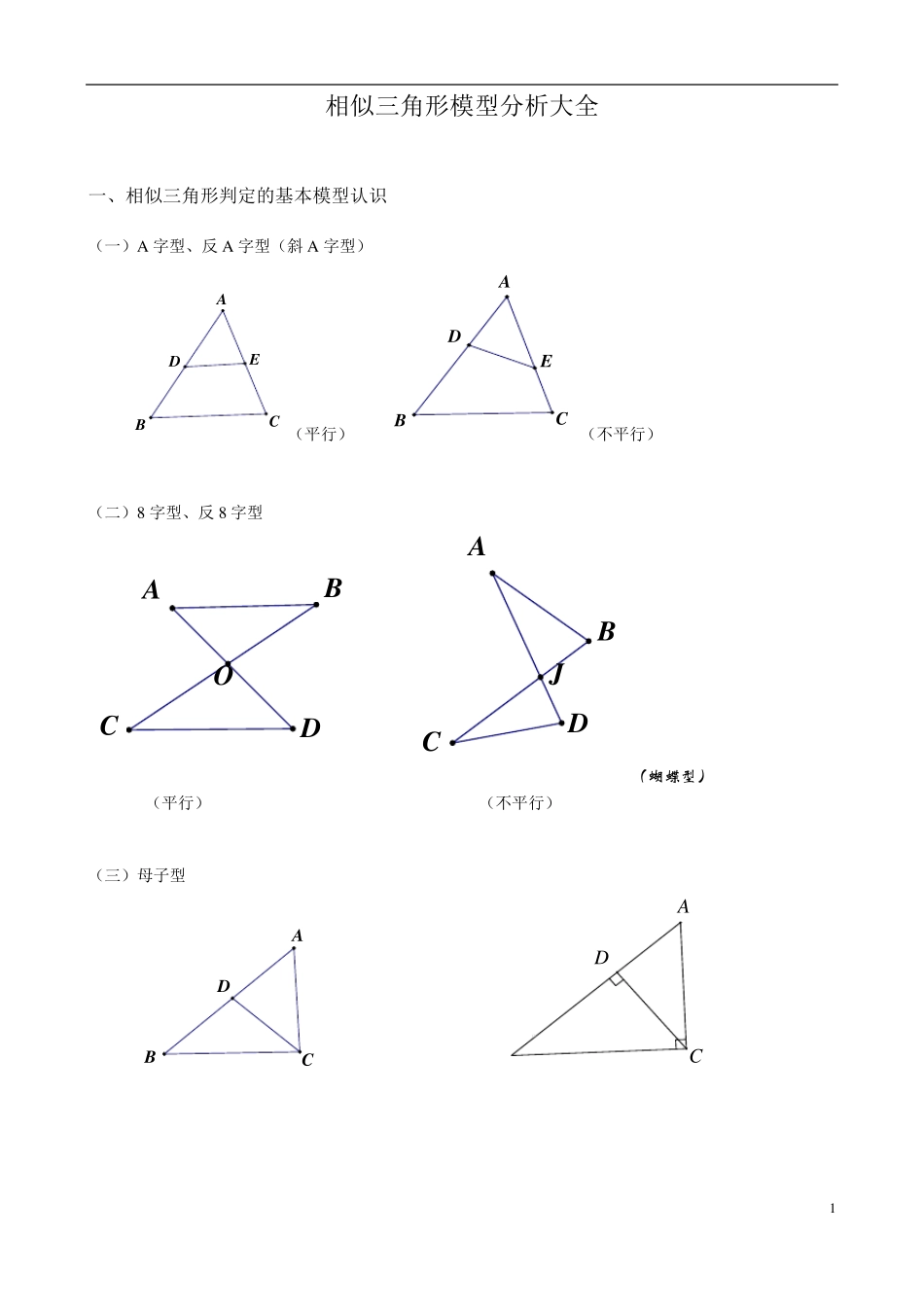
1 相似三角形模型分析大全 一、相似三角形判定的基本模型认识 （一）A 字型、反 A 字型（斜 A 字型） ABCDE（平行） CBADE（不平行） （二）8 字型、反 8 字型 JOADBCABCD（蝴蝶型） （平行） （不平行） （三）母子型 ABCD CAD 2 母子型相似三角形 例1 ：如图，梯形ABCD 中，AD∥BC，对角线 AC、BD 交于点 O，BE∥CD 交 CA 延长线于 E． 求证：OEOAOC2． 例2 ：已知：如图，△ABC 中，点 E 在中线 AD 上, ABCDEB． 求证：DADEDB2； 相关练习： 1 、如图，已知 AD 为△ABC 的角平分线，EF 为 AD 的垂直平分线．求证：FCFBFD2． A C D E B 3 2、已知：AD 是Rt△ABC 中∠A 的平分线，∠C=90°，EF 是AD 的垂直平分线交 AD 于 M，EF、BC 的延长线交于一点 N。 求证：(1)△AME∽△NMD; (2)ND 2 =NC·NB 4 3在 ABC 中，AB=AC，高AD与BE交于H，EF BC，垂足为F，延长AD到G，使DG=EF，M是AH的中点。 求证：GBM9 0 GMFEHDCBA 5 （四）一线三等角型： 三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景 （五）一线三直角型： 一线三等角型相似三角形 例1：如图，等边△ABC 中，边长为6，D 是BC 上动点，∠EDF=60° （1）求证：△BDE∽△CFD （2）当 BD=1，FC=3 时，求 BE C A D B E F 6 例2 ：已知在梯形ABCD 中，AD∥BC，AD＜BC，且AD＝5 ，AB＝DC＝2 ． （1 ）如图8 ，P 为AD 上的一点，满足∠BPC＝∠A． ①求证；△ABP∽△DPC ②求 AP 的长． （2 ）如果点P 在AD 边上移动（点P 与点A、D 不重合），且满足∠BPE＝∠A，PE 交直线 BC 于点E，同时交直线 DC 于点Q，那么当点Q 在线段 DC 的延长线上时，设 AP＝x，CQ＝y，求 y关于 x的函数解析式，并写出函数的定义域； C D A B P 7 8 9 相关练习： 1、如图，已知在△ABC 中， AB=AC=6，BC=5，D 是AB 上一点，BD=2，E是BC 上一动点，联结DE，并作DEFB，射线EF交线段AC 于F． （1）求证：△DBE∽△ECF； （2）当 F是线段AC 中点时，求线段BE的长； （3）联结DF，如果△DEF与△DBE相似，求FC 的长． FBACDE 10 2、已知在梯形ABCD 中，AD∥BC，AD＜BC，且BC =6，AB=DC=4，点E 是AB 的中点． （1）如图，P 为BC 上的一点，且BP=2．求证：△BEP∽△CPD； （2）如果点P 在BC 边上移...