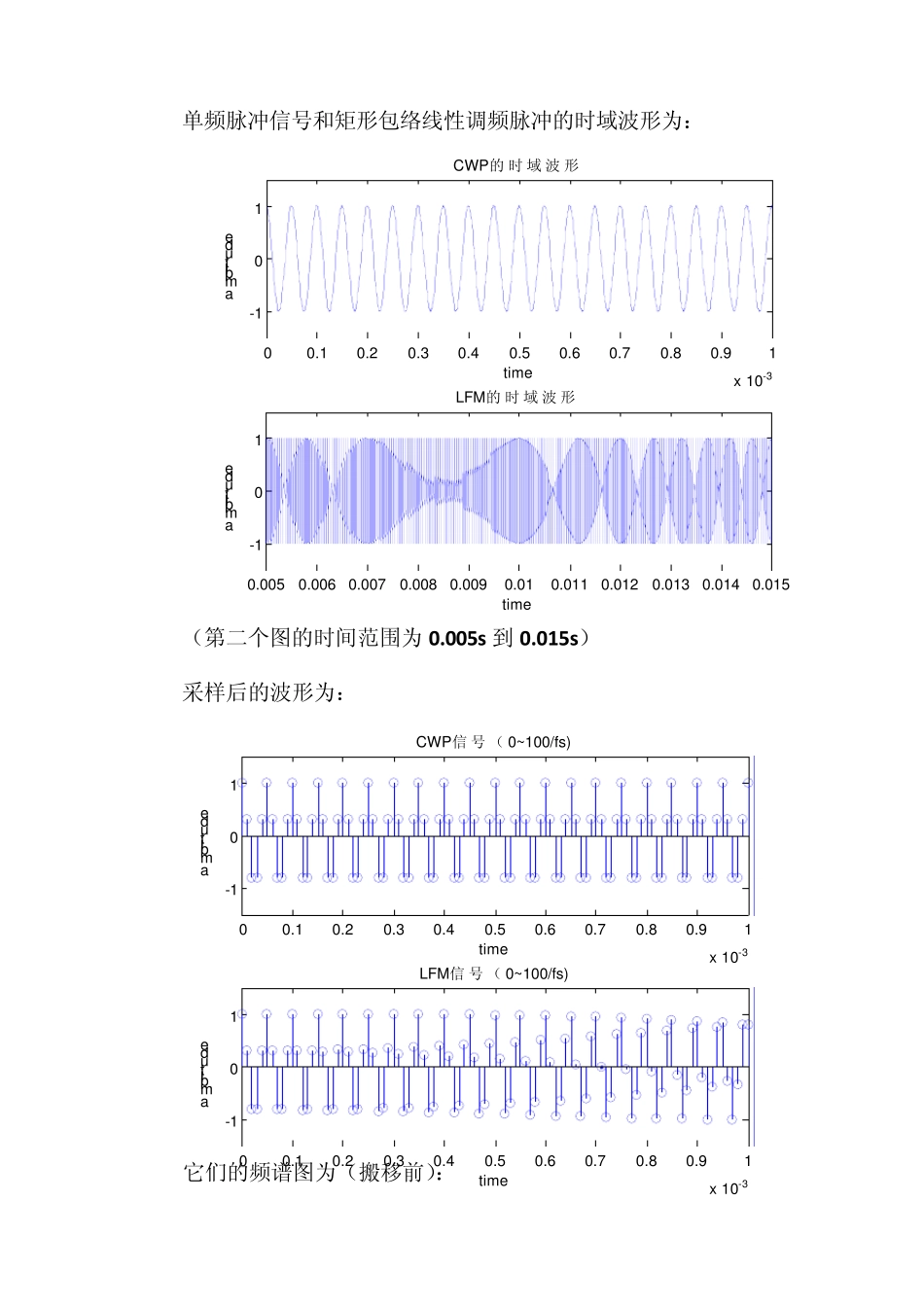
离散信号的产生和频谱分析 实验目的: 仿真掌握采样定理 学会用FFT 进行数字谱分析 掌握FFT 进行数字谱分析的计算机编程实现方法 培养学生综合分析、解决问题的能力、加深对课堂内容的理解 实验要求: 掌握采样定理和数字谱分析方法、编制 FFT 程序;完成正弦信号、线性条调频信号等模拟水声信号的数字谱分析; 实验内容: 单频脉冲(CWP)为)2exp()()(0tfjTtrectts。式中,)(Ttrect是矩形包络,T 是脉冲持续时间,0f 是中心频率。 矩 形 包 络 线 性 调 频脉 冲 信号( LFM ) 为)]21(2exp[)()(20MttfjTtrectts。式中, M 是线性调频指数。瞬时频率Mtf0是时间的线性函数,频率调制宽度为MTB 。 设参数为kHzf200 ,msT50,kHzB10,采样频率kHzfs100。 1.编程产生单频脉冲、矩形包络线性调频脉冲。 2.编程实现这些信号的谱分析。 3.编程实现快速傅立叶变换的逆变换。 实验步骤: 1.编程产生单频脉冲、矩形包络线性调频脉冲。 2.应用快速傅立叶变换(FFT)求这两种信号的频谱,分析离散谱位置、归一化频率、实际频率的关系。 调用函数Y=fft(x) or Y=fft(x,N) or Y=fft(x,N,dim)。 3.对于步骤 2 的结果,应用快速傅立叶变换的逆变换(IFFT)求两种信号的时域波形,并与已给的单频脉冲、矩形包络线性调频脉冲和伪随机脉冲信号波形进行对照。 调用函数x=ifft(Y) or x=ifft(Y,N) or x=ifft(Y,N,dim)。 4.对于步骤 2 的结果,进行频谱移位调整。将 FFT 变换的结果Y(频谱数据)进行移位调整,使其符合频谱常观表示方法,调整后,频谱的直流成分(即频率为 0 处的值)移到频谱的中间位置。分析离散谱位置、归一化频率、实际频率的关系。 移位调整调用函数Z=fftshift(Y)。频率间隔为 Fs/N,频率范围为Fs/N*[-N/2:N/2-1]。 实验结果: 单频脉冲信号和矩形包络线性调频脉冲的时域波形为: 00.10.20.30.40.50.60.70.80.91x 10-3-101timeamplitudeCWP的时域波形0.0050.0060.0070.0080.0090.010.0110.0120.0130.0140.015-101timeamplitudeLFM的时域波形 (第二个图的时间范围为0.005s到 0.015s) 采样后的波形为: 它们的频谱图为(搬移前): 00.10.20.30.40.50.60.70.80.91x 10-3-101timeamplitudeCWP信号(0~100/fs)00.10.20.30.40.50.60.70.80.91x 10-3-101timeamplitudeLFM信号(0~100/fs)-5-4-3-2-1012345x 1040200040006000f/Hzamplitude搬移前...