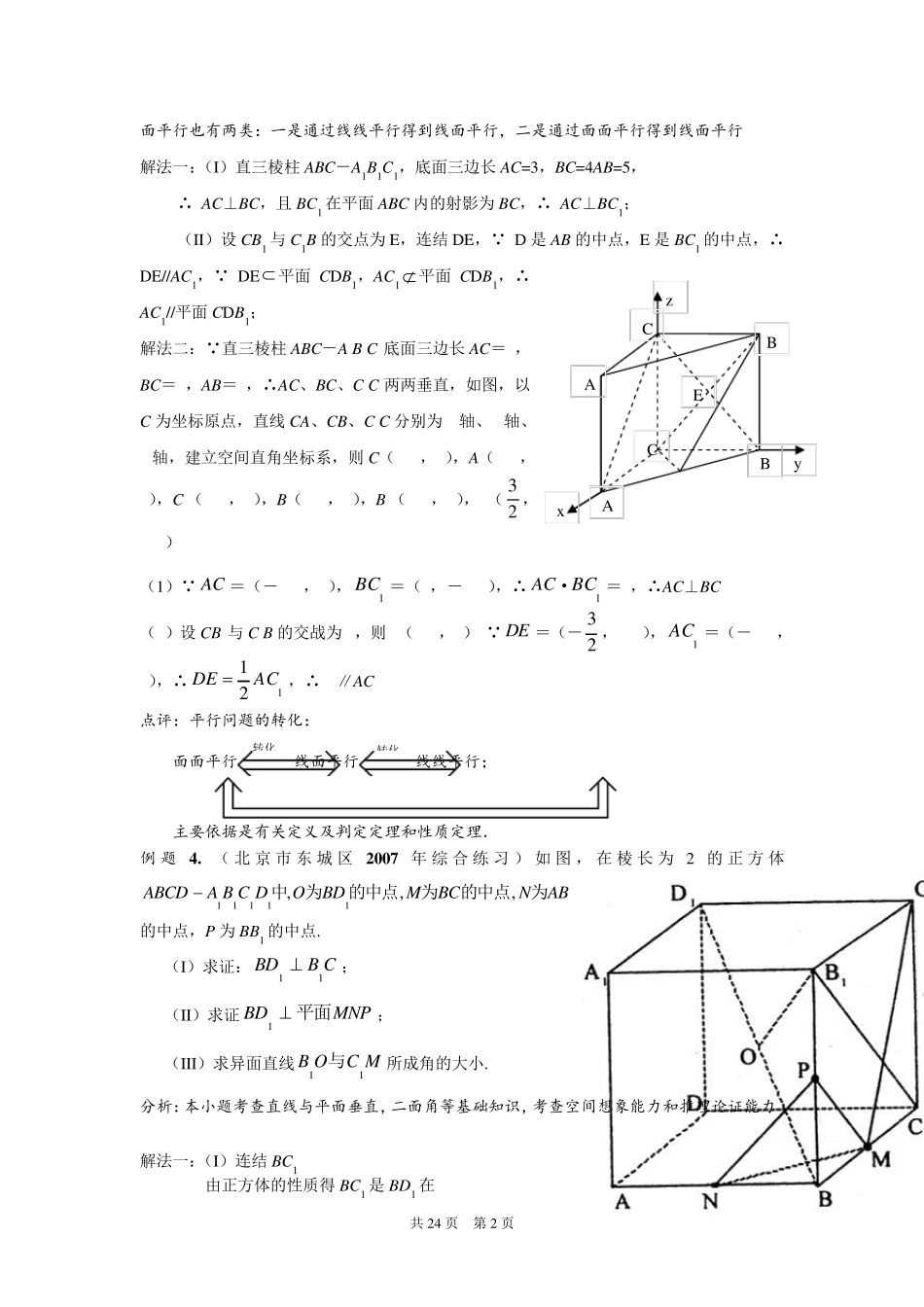
共24 页 第1 页 例题1. 已知, ,A B C 三点不共线,对平面外任一点,满足条件122555OPOAOBOC, 试判断:点P 与, ,A B C 是否一定共面? 分析:要判断点P 与, ,A B C 是否一定共面,即是要判断是否存在有序实数对 ,x y,使APxAByAC或对空间任一点O ,有OPOAxAByAC。 解:由题意:522OPOAOBOC, ∴()2()2()OPOAOBOPOCOP, ∴22APPBPC,即22PAPBPC , 所以,点P 与, ,A B C 共面. 点评:在用共面向量定理及其推论的充要条件进行向量共面判断的时候,首先要选择恰当的充要条件形式,然后对照形式将已知条件进行转化运算. 例题2. 如图,已知矩形 ABCD 和矩形 ADEF 所在平面互相垂直,点M ,N 分别在对角线BD ,AE 上,且13BMBD,13ANAE.求证://MN平面CDE . 分析:要证明//MN平面 CDE ,只要证明向量 NM 可以用平面CDE 内的两个不共线的向量 DE 和 DC 线性表示. 证明:如图,因为 M 在 BD 上,且13BMBD,所以111333MBDBDAAB.同理1133ANADDE,又CDBAAB ,所以 MNMBBAAN 1111()()3333DAABBAADDE2133BADE2133CDDE.又CD 与DE 不共线,根据共面向量定理,可知MN ,CD ,DE 共面.由于MN 不在平面CDE内,所以//MN平面CDE . 点评:空间任意的两向量都是共面的. 考点二 证明空间线面平行与垂直 例题3 . 如图, 在直三棱柱 ABC-A1B1C1 中,AC=3,BC=4,AA1=4,点D 是AB 的中点, (I)求证:AC⊥BC1; (II)求证:AC 1//平面CDB1; 分析:(1)证明线线垂直方法有两类:一是通过三垂线定理或逆定理证明,二是通过线面垂直来证明线线垂直;(2)证明线共24 页 第2 页 转化 转化 面平行也有两类:一是通过线线平行得到线面平行,二是通过面面平行得到线面平行. 解法一:(I)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4AB=5, ∴ AC⊥BC,且BC1 在平面ABC 内的射影为BC,∴ AC⊥BC1; (II)设CB1 与C1B 的交点为E,连结DE, D 是AB 的中点,E 是BC1 的中点,∴ DE//AC1, DE 平面CDB1,AC1 平面CDB1,∴ AC1//平面CDB1; 解法二: 直三棱柱ABC-A1B1C1底面三边长AC=3,BC=4,AB=5,∴AC、BC、C1C 两两垂直,如图,以C 为坐标原点,直线CA、CB、C1C 分别为x轴、y轴、z轴,建立空间直角坐标系,则C(0,0,0),A(3,0,0)...