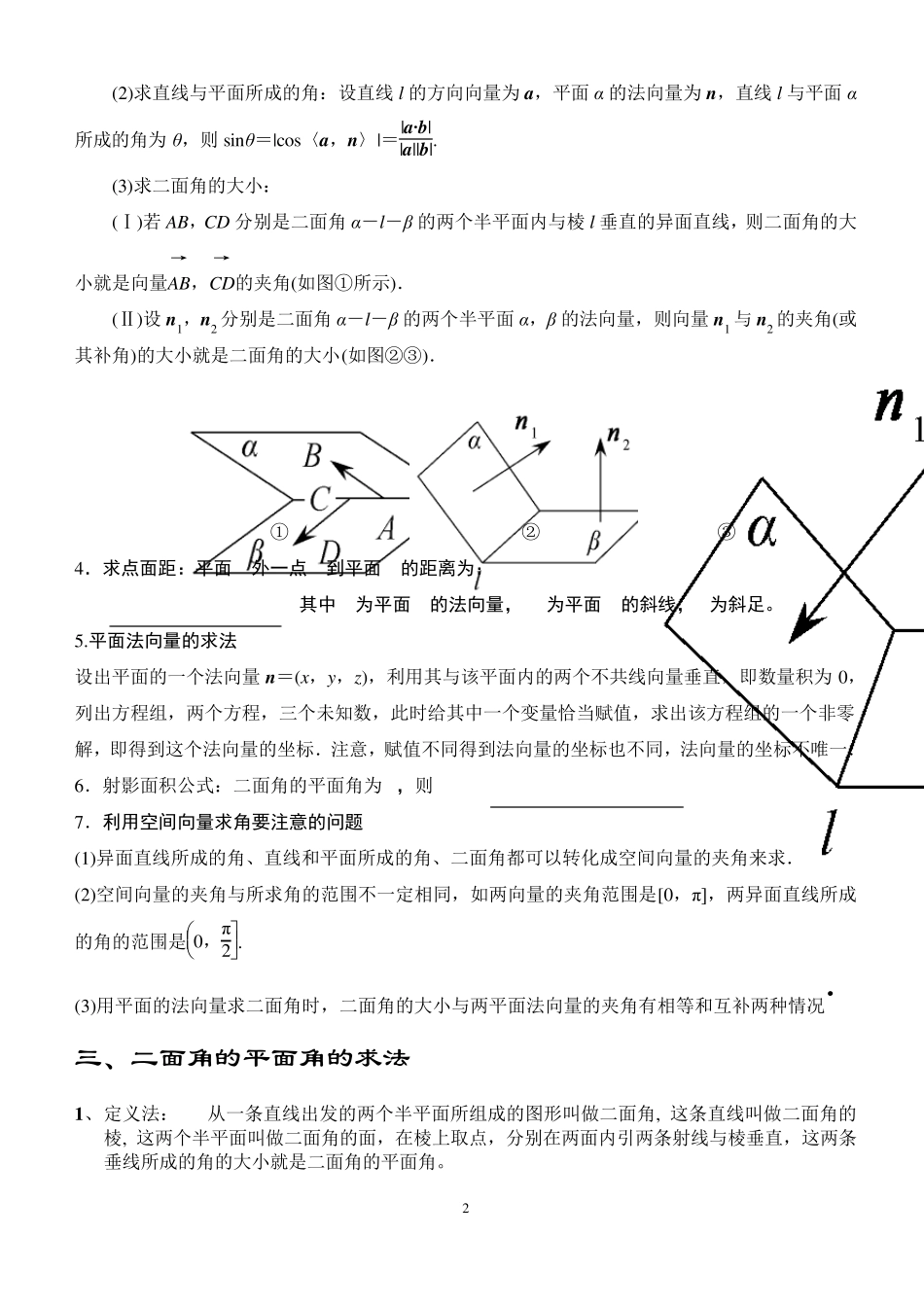
1 讲义:立体几何中的向量方法及二面角的平面角求法总结 一、几种角的范围 1、二面角平面角的范围: 2、线面角的范围: 3、直线倾斜角范围: 4、异面直线夹角范围: 5、向量夹角范围: 二、立体几何中的向量方法 1.三个重要向量 (1)直线的方向向量:直线的方向向量是指和这条直线平行(或重合)的向量,一条直线的方向向量有_______个. (2)平面的法向量:直线l⊥平面α,取直线l的方向向量,则这个向量叫做平面α 的法向量.显然一个平面的法向量有_____个,它们是共线向量. (3)直线的正法向量:直线L:Ax+By+C=0 的正法向量为n=(A,B). 2.直线的方向向量与平面的法向量在确定直线和平面位置关系中的应用 (1)直线l1 的方向向量为u1=(a1,b1,c1),直线l2 的方向向量为u2=(a2,b2,c2). 如果l1∥l2,那么 u1∥u2⇔u1=λu2⇔______________________________; 如果l1⊥l2,那么 u1⊥u2⇔u1·u2=0⇔_____________________. (2)直线l的方向向量为u=(a1,b1,c1),平面α 的法向量为n=(a2,b2,c2). 若 l∥α,则u⊥n⇔u·n=0⇔______________________. 若 l⊥α,则u∥n⇔u=kn⇔__________________________. (3)平面α 的法向量为u1=(a1,b1,c1),平面β 的法向量为u2=(a2,b2,c2). 若 α∥β,u1∥u2⇔u1=ku2⇔(a1,b1,c1)=______________; 若 α⊥β,则u1⊥u2⇔u1·u2=0⇔________________________. 3.利用空间向量求空间角 (1)求两条异面直线所成的角:设 a,b 分别是两异面直线l1,l2 的方向向量,则 3-4 课时 2 (2)求直线与平面所成的角:设直线l 的方向向量为a,平面α 的法向量为n,直线l 与平面α所成的角为θ,则sinθ=|cos〈a,n〉|=|a·b||a||b|. (3)求二面角的大小: (Ⅰ)若 AB,CD 分别是二面角α-l-β 的两个半平面内与棱 l 垂直的异面直线,则二面角的大小就是向量AB→,CD→的夹角(如图①所示). (Ⅱ)设n1,n2 分别是二面角α-l-β 的两个半平面α,β 的法向量,则向量n1 与n2 的夹角(或其补角)的大小就是二面角的大小(如图②③). ① ② ③ 4.求点面距:平面a外一点P到平面a的距离为: d= 其中n为平面a的法向量,PQ为平面a的斜线,Q为斜足。 5.平面法向量的求法 设出平面的一个法向量n=(x,y,z),利用其与该平面内的两个不共线向量垂直,即数量积为0,列出方程组,两个方程,三个未知数,此时给其中一个变量恰当赋值,求出该方...