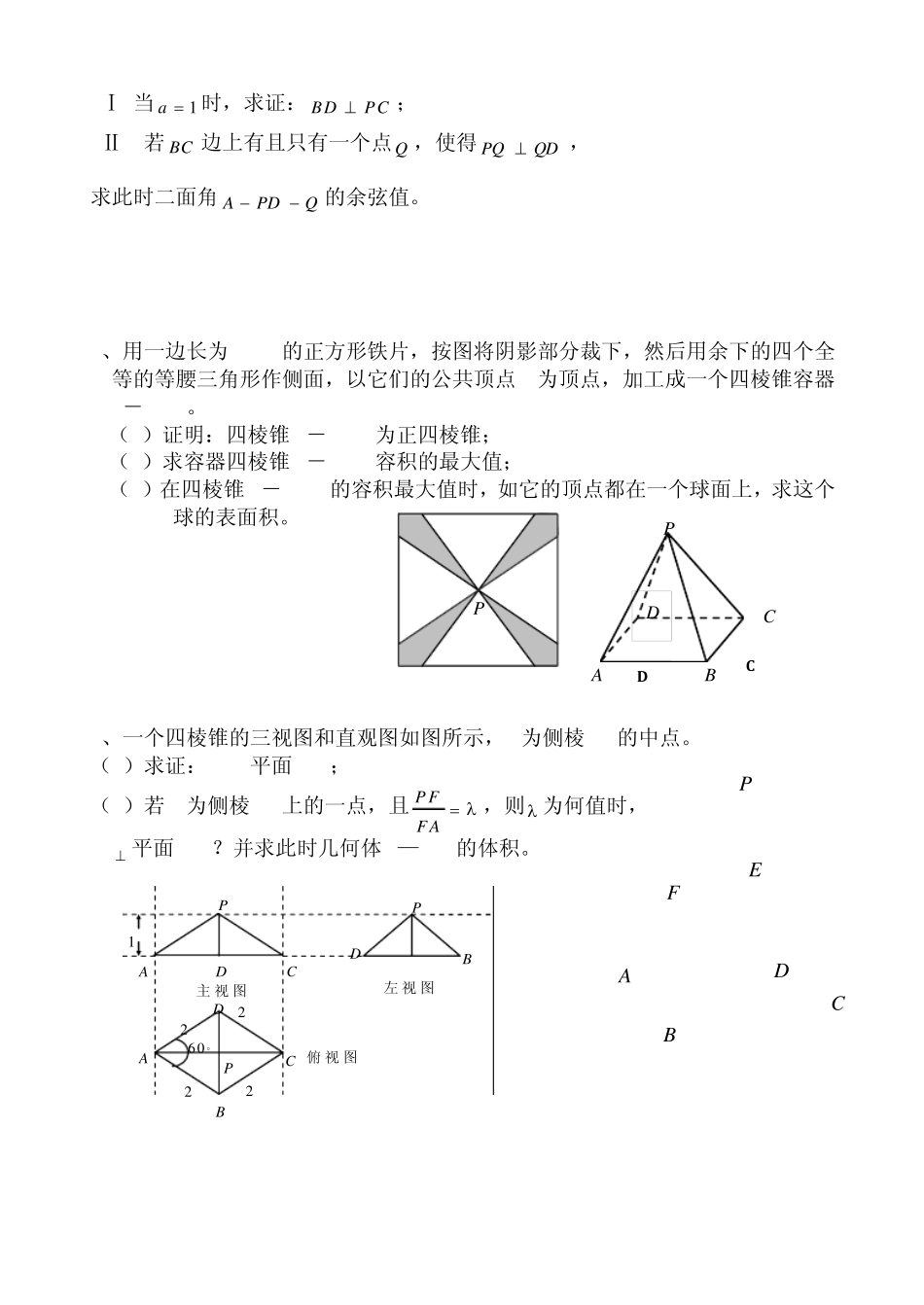
P A B C D Q GFDECBA立体几何(创新题) 1、如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥底面ABC (1)当k=21 时,求直线PA与平面PBC所成角的正弦值。 (2)当k取何值时,O在平面PBC内的射影恰好为△PBC的重心? 2、如图,在矩形ABCD中,AB=2,BC=a ,又PA⊥平面ABCD,PA=4. (1)BC上存在一点Q,使PQ⊥QD,求a 的取值范围; (2)C上存在唯一点Q,使PQ⊥QD时,求二面角 A-PD-Q的余弦值。 3、已知梯形ABCD中,AD∥BC,∠ABC =∠BAD =2 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x ,G是BC的中点。沿 EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图) 。 (1) 当x =2时,求证:BD⊥EG ; (2) 若以 F、B、C、D为顶点的三棱锥的体积记为( )fx ,求( )fx 的最大值; (3) 当( )fx 取得最大值时,求二面角D-BF-C的余弦值。 4、在四 棱锥A B C DP 中,PA平面A B C D,底面A B C D 为矩形,)0(aa B CPAAB。 ABCDOPAABCDPPDDBCP1222260 主视图左视图俯视图ABCDFEP(Ⅰ)当1a 时,求证:BDPC; (Ⅱ) 若BC 边上有且只有一个点Q ,使得QDPQ , 求此时二面角QPDA的余弦值。 5、用一边长为12cm的正方形铁片,按图将阴影部分裁下,然后用余下的四个全等的等腰三角形作侧面,以它们的公共顶点P为顶点,加工成一个四棱锥容器P-ABCD。 (1)证明:四棱锥P-ABCD为正四棱锥; (2)求容器四棱锥P-ABCD容积的最大值; (3)在四棱锥P-ABCD的容积最大值时,如它的顶点都在一个球面上,求这个球的表面积。 6、一个四棱锥的三视图和直观图如图所示,E为侧棱PD的中点。 (1)求证:PB//平面AEC; (2)若F为侧棱PA上的一点,且PFFA,则 为何值时, PA 平面BDF?并求此时几何体F—BDC的体积。 C D P A B C D P 参考答案 1、(1)30210 (2)1k 2、解法1:(Ⅰ)如图,连 AQ ,由于 PA⊥平面 ABCD,则由 PQ⊥QD,必有 AQDQ. 设 BQt ,则 CQat , 在 Rt ABQ中,有24AQt. 在 Rt CDQ中,有24DQat. 在 Rt ADQ中,有222AQDQAD. 即22244tata,即240tat. ∴44att. 故 a 的取值范围为4, . (Ⅱ)由(Ⅰ)知,当2t ,4a 时,边 BC上存在唯一点 Q(Q为 BC边的中点), 使 PQ⊥...