立体几何大题线面角训练1

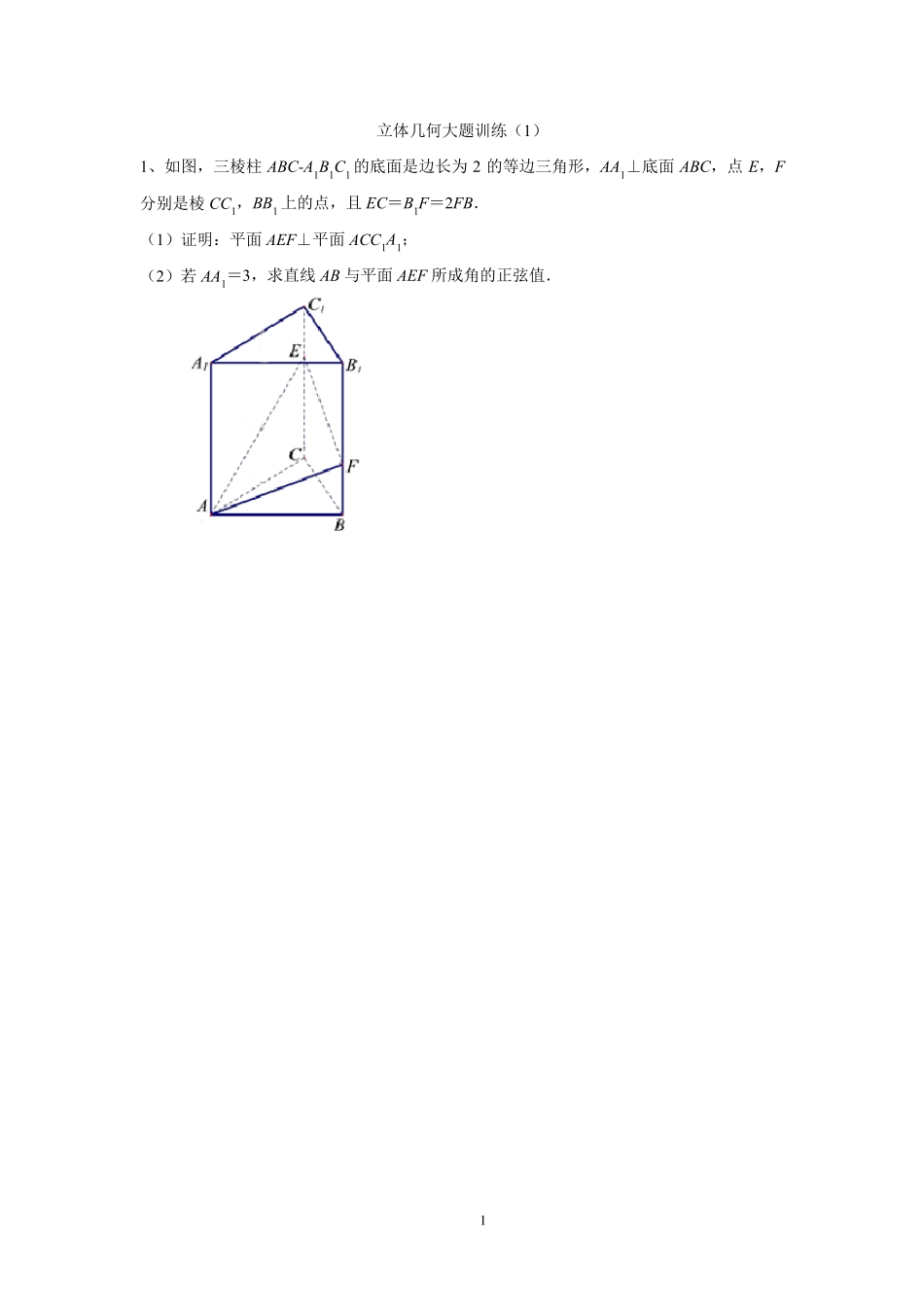
1 立体几何大题训练（1） 1、如图，三棱柱ABC-A1B1C1 的底面是边长为2 的等边三角形，AA1⊥底面ABC，点 E，F分别是棱CC1，BB1 上的点，且 EC＝B1F＝2FB． （1）证明：平面AEF⊥平面ACC1A1； （2）若 AA1＝3，求直线 AB 与平面AEF 所成角的正弦值． 2 2、如图，在四棱锥ABCDP中，AB平面 BCP，//CD平面 ABP， 22CDBPCPBCAB． （1）证明：平面BAP平面 DAP； （2）点 M 为线段 AB（含端点）上一点，设直线 MP与平面 DCP所成角为 ，求sin的取值范围． 3 3、如图，四棱锥ABCDP中，底面 ABCD为菱形，PA底面 ABCD，22AC，2PA， E是 PC 上的一点，ECPE2． （1）证明：PC平面 BED ； （2）设二面角CPBA为9 0 ，求直线 PD 与平面PBC所成角的大小． 4 4、如图，在四棱锥 P ABCD中，底面 ABCD 是平行四边形，1 3 5BCD，侧面 PAB 底面 ABCD ，9 02BAPABACPAEF，， ，分别为 BCAD，的中点，点 M在线段 PD 上． （1）求证： EF  平面 PAC ； （2）如果直线 ME 与平面 PBC 所成的角和直线 ME 与平面 ABCD 所成的角相等，求PMPD的值． 5 5、在四边形ABCD 中，对角线,AC BD 垂直相交于点O ，且4OAOBOD，3OC ．将BCD△沿BD 折到BED△的位置，使得二面角EBDA的大小为9 0 （如图）．已知Q 为EO的中点，点P 在线段AB 上，且 2AP ． （1）证明：直线PQADE∥平面； （2）求直线BD 与平面ADE 所成角 的正弦值． 6 6 、如图，已知矩形ABCD 中，43ABAD，，现将DAC沿着对角线AC 向上翻折到PAC 位置，此时PAPB． （Ⅰ）求证：平面 PAB  平面 ABC （Ⅱ）求直线AB 与平面 PAC 所成的正弦值． ABCPDCBA 7 7、如图，六面体HEFGABCD 中，四边形 ABCD为菱形，DHCGBFAE,,,都垂直于平面 ABCD.若4DBDHDA,3 CGAE. （1）求证：DFEG ; （2）求 BE 与平面 EFGH 所成角的正弦值. 8 8、如图，在底面是平行四边形的四棱锥PABCD中，,E F分别是,AB PC 的中点，平面PDE  平面PCD,1PDDE ,2PEAB. （Ⅰ）证明：直线/ /BF面PDE （Ⅱ）求直线 PA 与平面PBC 所成角的正弦值.