第2课_平行线分线段成比例定理及其推论

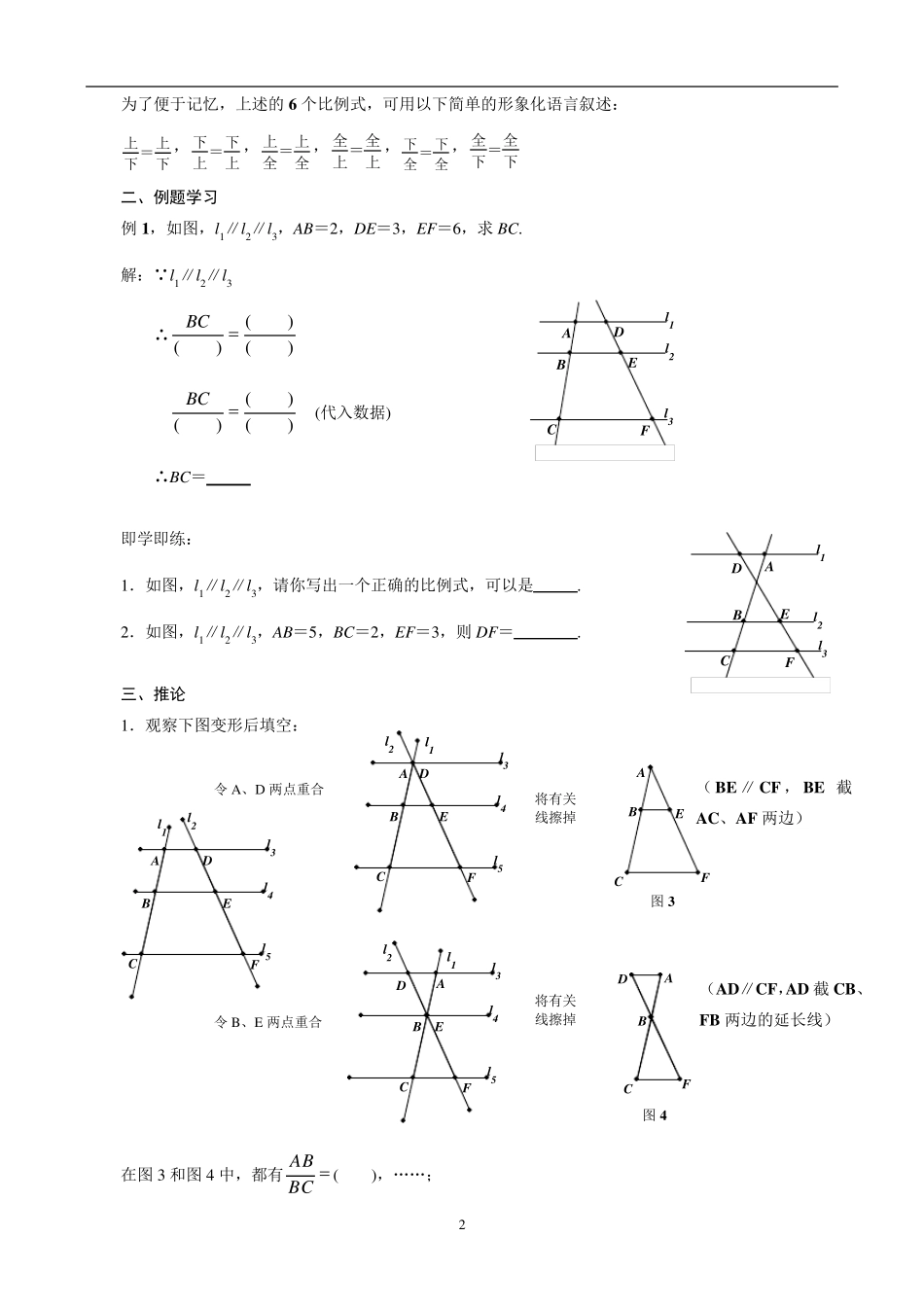
1 l5l3l4EBFDCAl5l3l4FEDCBA（1）平行线分线段成比例定理及其推论 学习目标： 1 ．在理解的基础上掌握平行线分线段成比例定理，并会灵活应用． 2 ．在巩固平行线等分线段定理的基础上掌握其推论及推论的应用． 新课学习： 一、探究 1 ．如图，线段BE 为梯形ACFD 的中位线， 由此可知：①l3 l4 l5； ② BCAB( )，EFDE( ) ∴BCAB EFDE；（填“＝”或“≠” ） 2 ．如图，线段BE 不再是梯形ACFD 的中位线，而直线l3∥l4∥l5 ，若 AB＝m，BC＝n， 由此可知：BCAB( ) 猜想：EFDE( )， 也就是我们认为：BCAB EFDE； 3 ．总结： 如图2 ， l3∥l4∥l5 ∴BCAB( )，ABBC( )，ACAB( )， ABAC( )，ACBC( )，BCAC( )； 平行线分线段成比例定理： 三条 截两条直线，所得的 线段成比例．．．． l3l4l5l1l2l5l3l4EBFEDCBAFDCA梯形延伸 图1 图2 2 为了便于记忆，上述的6 个比例式，可用以下简单的形象化语言叙述： 下上＝下上，上下＝上下，全上＝全上，上全＝上全，全下＝全下，全全＝下下 二、例题学习 例1，如图，l1∥l2∥l3，AB＝2，DE＝3，EF＝6，求BC. 解： l1∥l2∥l3 ∴) () () (BC ) () () (BC (代入数据) ∴BC＝ 即学即练： 1．如图，l1∥l2∥l3，请你写出一个正确的比例式，可以是 . 2．如图，l1∥l2∥l3，AB＝5，BC＝2，EF＝3，则DF＝ . 三、推论 1．观察下图变形后填空： 在图3 和图4 中，都有BCAB( )，……； l3l4l5l1l2l3l4l5l1l2l3l4l5l1l2FDCBAFEDCBAFECBAFEDCBAFEDCBA令 A、D 两点重合 令 B、E两点重合 将有关 线擦掉 将有关 线擦掉 （ BE ∥CF，BE 截AC、AF 两边） （AD∥CF，AD 截 CB、FB 两边的延长线） 图3 图4 l1l2l3FEDCBAl1l2l3FEDCBA 3 l1l2l3FDAECBl1l2l3FDBECA2．总结： 几何语言： BE∥CF（或AD∥CF） ∴ EFAEBCAB …… 四、例题学习 例 2，已知：如图，DE∥BC，AB=15，AC=9，BD＝4，求：AE． 解： DE∥BC ∴) () (AC CE ) () () (CE (代入数据) ∴CE＝ ∴AE＝ ＋ ＝ 五、课堂练习 A 组： 1．如图，已知 l1//l2//l3，下列比例式中错误的是（ ） A、DFBDCEAC  B、BFBDAEAC  C、BFDFAECE  D、ACBDBFAE  2．如图，已知 l1//l2//l3，下列比例式中成立的是（ ） A、BCCEDFAD  B、AFBCBEAD  C、BCADDFCE  D、CEBEDFAF  推论...