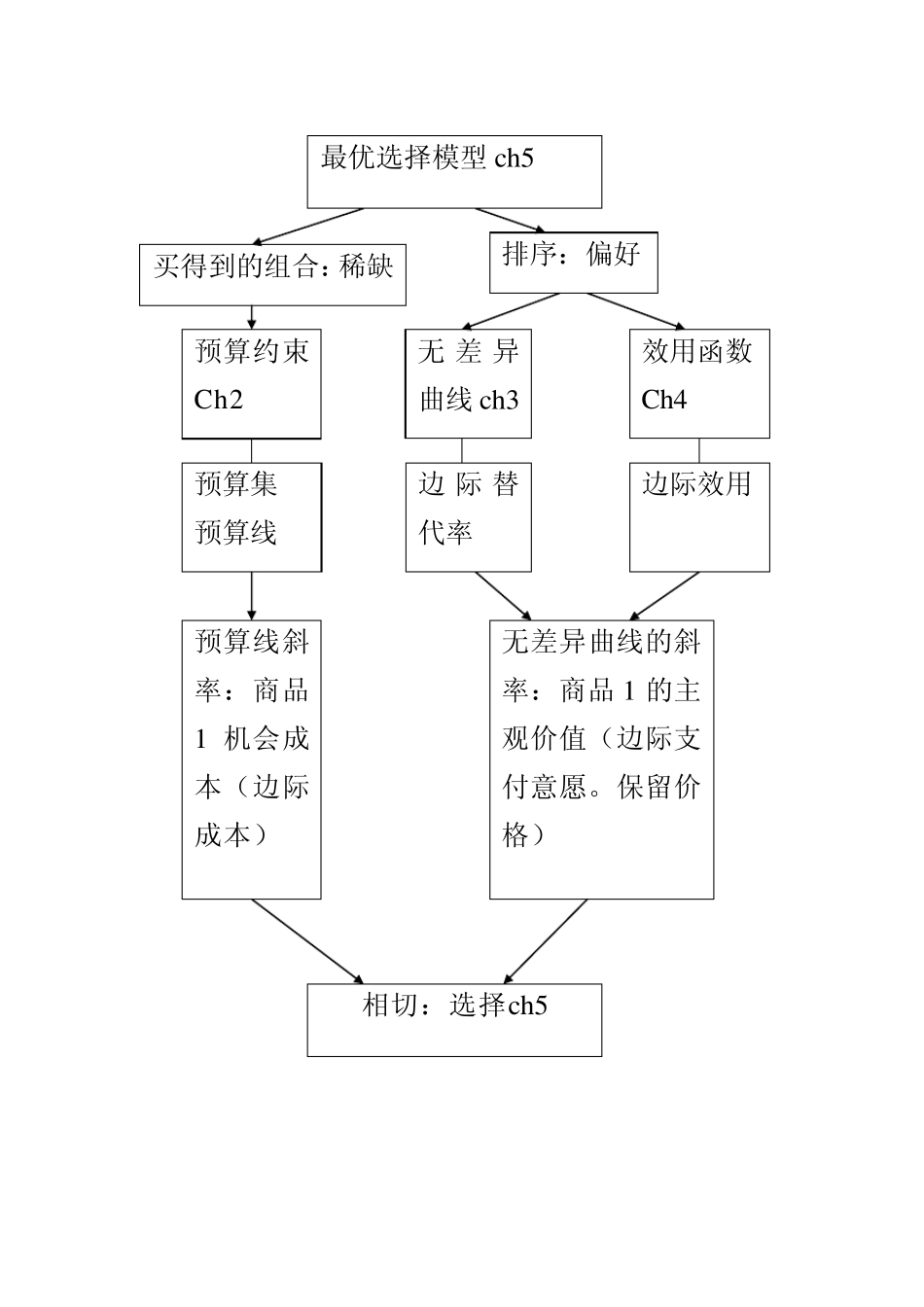
复习第2 讲,消费者最优化 2 .1 预算 2 .2 偏好 2 .3 效用 2 .4 选择 消费者最优——买得到的组合中选择最好的一个。 2 .1 预算:买得到的组合——预算可行集——稀缺性 预算线的斜率——机会成本。 2 .2 偏好:如何对可能消费的组合排序呢——偏好 无差异曲线,并假设理性、连续、单调、凸性排除了非理性的排序 2 .3 效用:更简便的排序是用效用函数 效用函数不唯一、但是有相同的边际替代率,边际替代率是无差异曲线的斜率——边际支付意愿或保留价格 2 .4 选择:通过排序我们可以找到最佳的消费组合 最优化模型的解满足相切条件,就是对商品 1 的边际支付意愿等于其机会成本。 但是并非满足相切条件的解是最优解。偏好是严格凸性的,也就是效用函数必须是严格拟凹的,此时满足一阶相切条件的解是最优解。 最优选择模型ch5 买得到的组合:稀缺 排序:偏好 无差异曲线ch3 效用函数 Ch4 边际替代率 边际效用 预算集 预算线 预算约束Ch2 相切:选择ch5 预算线斜率:商品1 机会成本(边际成本) 无差异曲线的斜率:商品1 的主观价值(边际支付意愿。保留价格) 第3 讲:效用最大化与支出最小化(补充) 3 .1 效用最大化 3 .2 支出最小化 3 .3 效用最大化与支出最小化:对偶关系 3 .1 效用最大化 Max U=U(x 1, x 2) S.t. P1 x 1 + P2 x 2 = M L=U(x 1, x 2) –ζ (P1 x 1 + P2 x 2 – M) L’x 1= ð U/ð x 1 –ζ P1=0……………(1) L’x 2 = ð U/ð x 2 –ζ P2=0……………(2) L’ζ =M – P1 x 1 – P2 x 2=0……………(3) x 1*=x 1(p1,p2,M),x 2*=x 2(p1,p2,M); 这是马歇尔需求函数 例子1 : U(x 1, x 2)= x 11/2 x 21/2 x 1*=(1/2) (m/p1),x 2*=(1/2) (m/p2) 如果价格和收入同比例变化,需求量保持不变。即马歇尔需求函数是零次齐次函数 x 1(tp1,tp2,tM)=t0x 1(p1,p2,M)=x 1(p1,p2,M) 例子2: 把马歇尔需求函数x 1*=(1/2) (m/p1),x 2*=(1/2) (m/p2) 代入U(x 1, x 2)= x 11/2 x 21/2 得到最大的效用U*= (1/2) p1-1/2 p2-1/2 m V= U*=V(p1, p2, m) =(1/2) p1-1/2 p2-1/2 m 我们把V=V(p1, p2, m)称为间接效用函数,把U=U(x 1, x 2)称为直接效用函数。间接效用函数相当于说,只要知道收入和价格,就知道相应的最大效用。那么...