自动控制原理MATLAB仿真实验报告

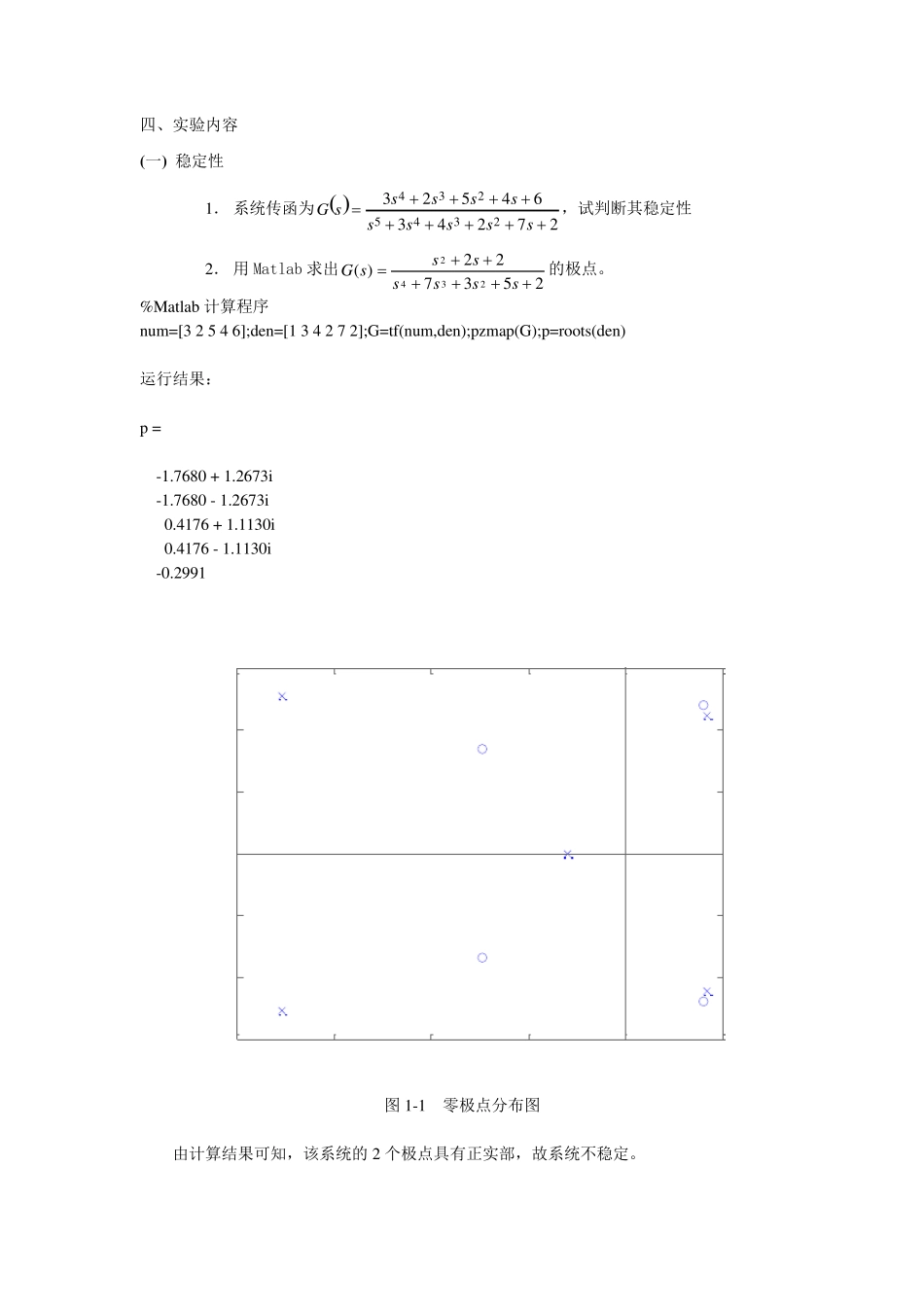
自 动 控 制 原 理 实 验 报 告 学 院 电子信息与电气工程学院 实验一 MATLAB 及仿真实验（控制系统的时域分析） 一、实验目的 学习利用MATLAB 进行控制系统时域分析，包括典型响应、判断系统稳定性和分析系统的动态特性； 二、预习要点 1、 系统的典型响应有哪些？ 2、 如何判断系统稳定性？ 3、 系统的动态性能指标有哪些？ 三、实验方法 （一） 四种典型响应 1、 阶跃响应： 阶跃响应常用格式： 1、 )(sysstep；其中sys 可以为连续系统，也可为离散系统。 2、),(Tnsysstep；表示时间范围0---Tn。 3、),(Tsysstep；表示时间范围向量T 指定。 4、),(TsysstepY ；可详细了解某段时间的输入、输出情况。 2、 脉冲响应： 脉冲函数在数学上的精确定义：0,0)(1)(0txfdxxf 其拉氏变换为：)()()()(1)(sGsfsGsYsf 所以脉冲响应即为传函的反拉氏变换。 脉冲响应函数常用格式： ① )(sysimpulse； ② );,();,(TsysimpulseTnsysimpulse ③ ),(TsysimpulseY  （二） 分析系统稳定性 有以下三种方法： 1、 利用pzmap 绘制连续系统的零极点图； 2、 利用tf2zp 求出系统零极点； 3、 利用roots 求分母多项式的根来确定系统的极点 （三） 系统的动态特性分析 Matlab 提供了求取连续系统的单位阶跃响应函数step、单位脉冲响应函数impulse、零输入响应函数initial 以及任意输入下的仿真函数lsim. 四、实验内容 (一) 稳定性 1． 系统传函为  27243645232345234ssssssssssG，试判断其稳定性 2． 用 Matlab 求出253722)(2342sssssssG的极点。 %Matlab 计算程序 num=[3 2 5 4 6];den=[1 3 4 2 7 2];G=tf(num,den);pzmap(G);p=roots(den) 运行结果： p = -1.7680 + 1.2673i -1.7680 - 1.2673i 0.4176 + 1.1130i 0.4176 - 1.1130i -0.2991 P ole-Zero MapReal AxisImaginary Axis-2-1.5-1-0.500.5-1.5-1-0.500.511.5 图 1-1 零极点分布图 由计算结果可知，该系统的 2 个极点具有正实部，故系统不稳定。 %求取极点 nu m=[1 2 2];den=[1 7 3 5 2];p=roots(den) 运行结果： p = -6.6553 0.0327 + 0.8555i 0.0327 - 0.8555i -0.4100 故253722)(2342sssssssG的极点s1=-6.6553 , s2=0.0327 + 0.8555i , s3= 0.0327 - 0.8555i , s4=-0.41 ...