自控非线性习题

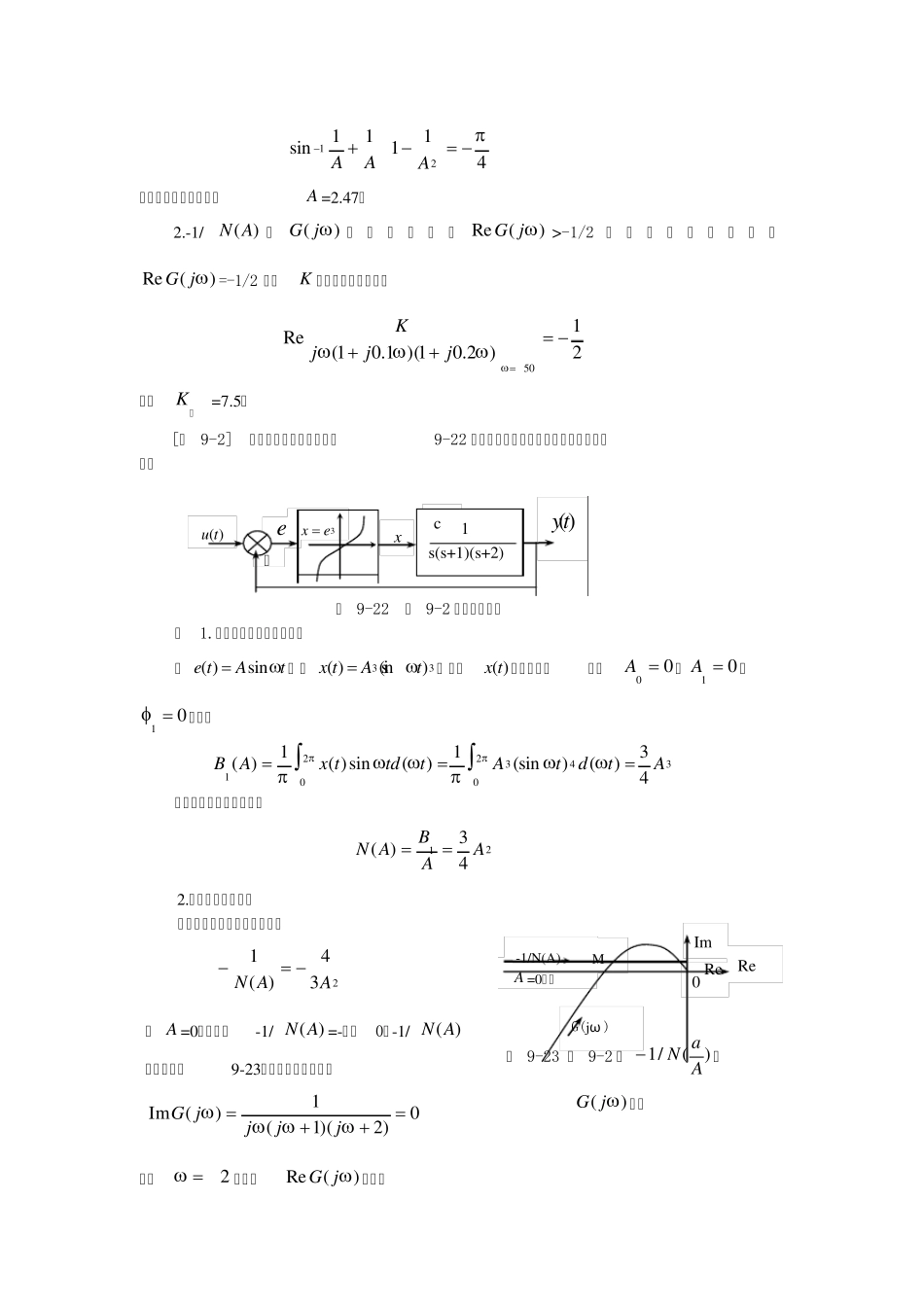
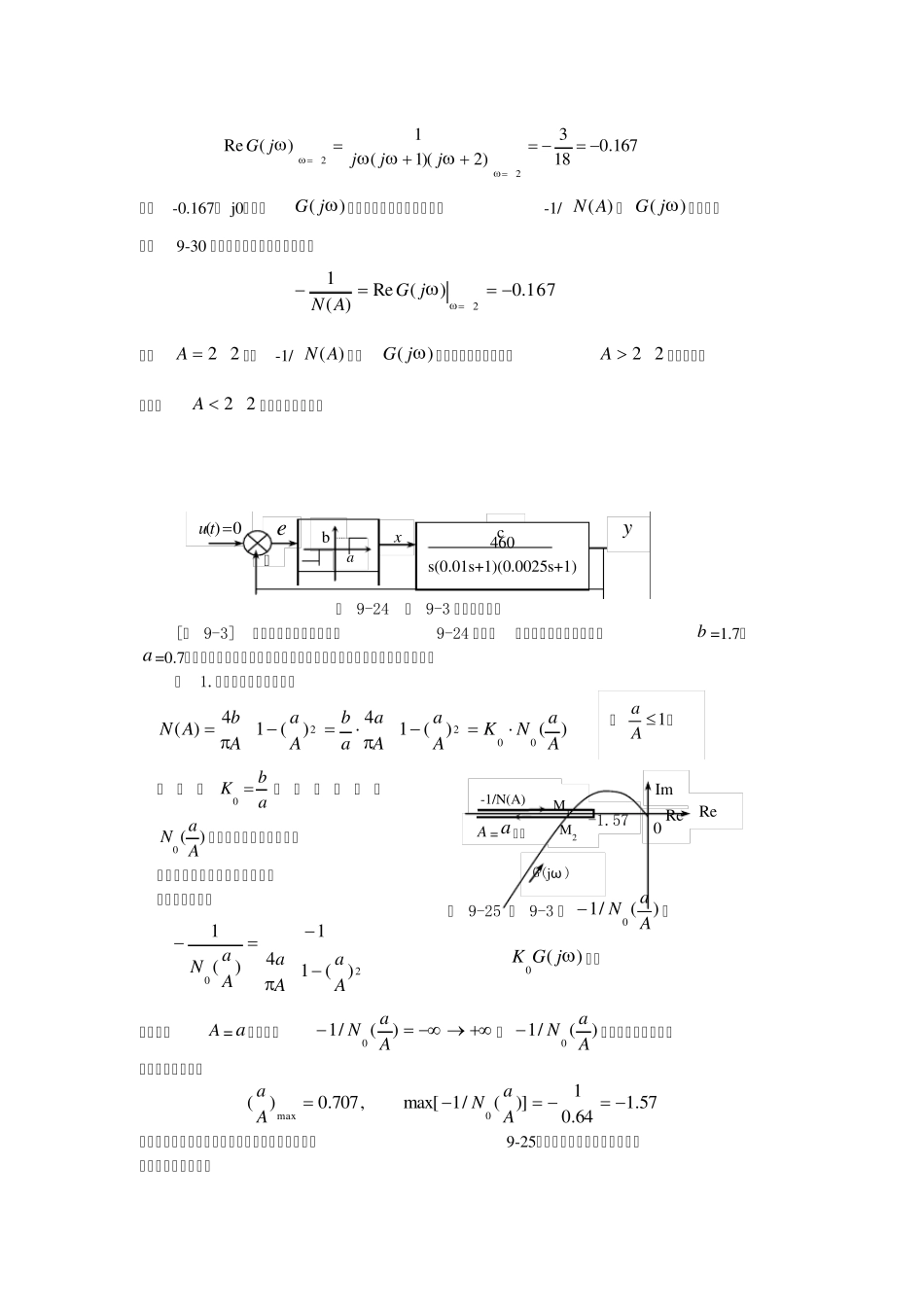
[例 9-1] 具有饱和非线性元件的非线性控制系统如图9-20 所示，（ 1）当线性部分 K =5 时，确定系统自振荡的幅值和频率。（ 2)确定系统稳定时，K 的临界值。 图 9-20 例 9-1 的系统结构图 解 1.在复平面上分别绘制-1/)(AN曲线和)( jG曲线。 饱和非线性特性的描述函数为 21)(1sin2)(AaAaAaKAN 由于非线性特性可知K=2， a=1，将a 和 K 代入上式，则得负倒数描述函数 211111sin4)(1AAAAN 图 9-21 例 9-1 的奈氏图 因饱和特性为单值特性，)(AN和 -1/)(AN为实函数。当 A =1～∞时，-1/ )(AN=-1/2～∞。-1/ )(AN曲线示于图9-21。由 0)0004.005.01()02.01(15)(Im422jG 解得50，代入)(RejG求得， 10004.005.015.4)(Re504250jG 则（-1， j0）点为)( jG曲线与负实轴的交点，亦是-1/ )(AN和)( jG的交点，如图9-21 所示。因-1/ )(AN穿出)( jG，故交点为自振点。自振频率50, 自振振幅由下列方程解出 1)(Re)(150jGAN 1]1111[sin421AAA u ex2 1 c —K s(0.1s+1)(0.2s+1) （aA） G(jω ) -1/N(A) K=7.5 -0.5 K=15 Re 0 Im y 41111sin21AAA 用试算法或作图法解得A =2.47。 2.-1/ )(AN与)( jG的 不 相 交 ， 即)(RejG>-1/2 时 ， 系 统 退 出 自 振 。)(RejG=-1/2 时的K 值为临界放大倍数。 21)2.01)(1.01(Re50jjjK 解得临K =7.5。 [例 9-2] 非线性系统的结构图如图9-22 所示，用描述函数法判断该系统的稳定性。 图 9-22 例 9-2 的系统结构图 解 1.求非线性部分的描述函数 设tAtesin)(， 则33)(sin)(tAtx； 因此)(tx是奇函数，故有00 A，01 A，01 ，其中 3204320143)()(sin1)(sin)(1)(AtdtAttdtxAB 非线性部分的描述函数为 2143)(AABAN 2.判断系统的稳定性 描述函数的相对负倒数特性为 234)(1AAN 当 A =0～∞时，-1/ )(AN=-∞～0。-1/ )(AN曲线示于图9-23，为整个负实轴。由 0)2)(1(1)(ImjjjjG 图 9-23 例 9-2 的)(/1AaN和)( jG曲线 解得2，代入)(RejG求得， )(ty )(tu ex3ex c —1 s(s+1)(s+2) Re G(jω ) -1/N(A) M A =0～∞ Re 0 I...