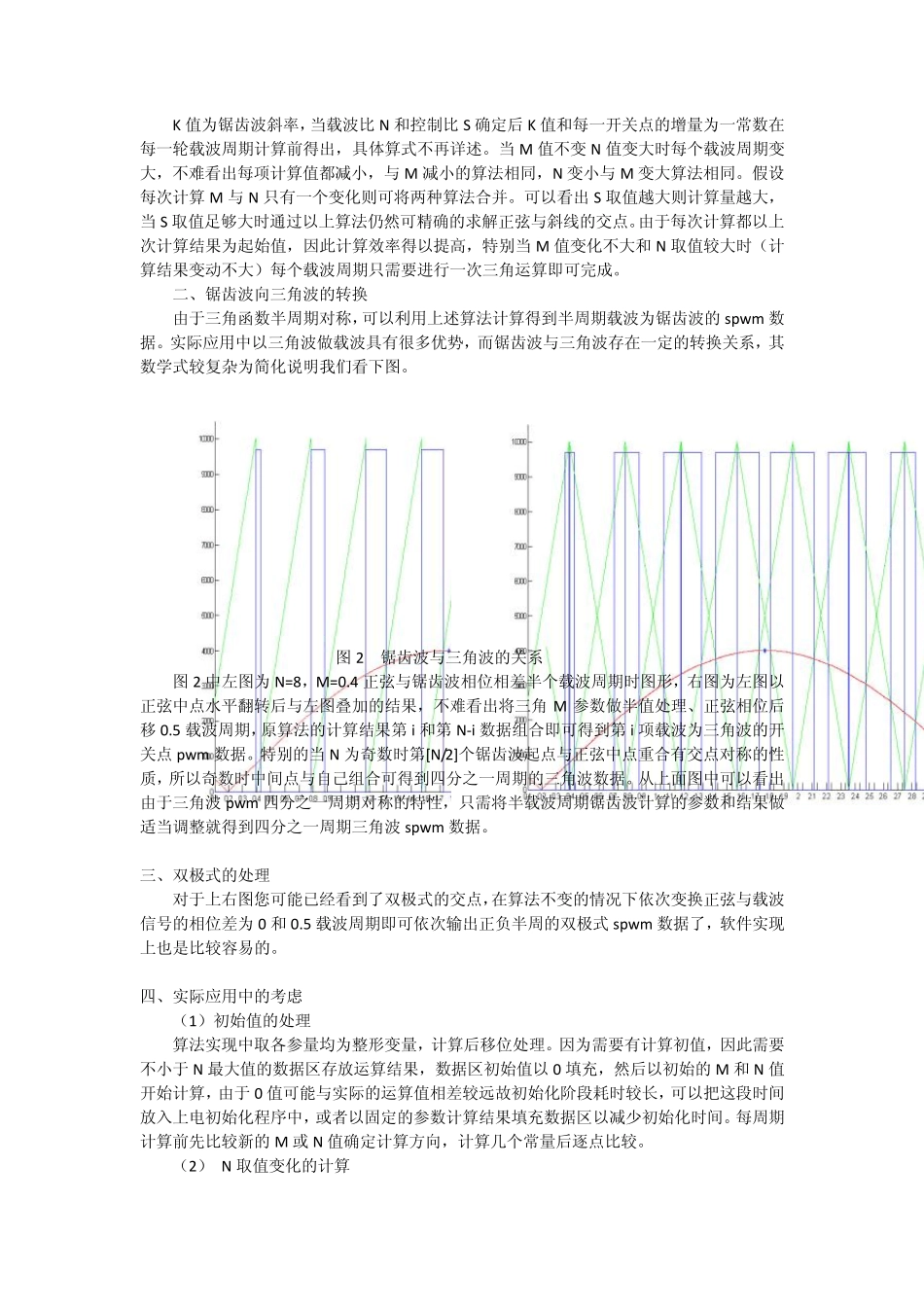
软件快速生成自然采样法SPWM 数据 引言: SPWM 即正弦脉宽调制技术在电力电子及工业控制领域有着广泛的应用,其波形的产生可分为硬件和软件两种方法,通过软件计算波形开关点实施调控具有电路简单、调控准确、应用灵活等优点。其软件算法中以自然采样法输出 SPWM 波形最接近正弦波,但由于三角波与正弦波交点有任意性,脉冲中心在一个周期内不等距,从而脉宽表达式是一个超越方程,计算式复杂。本文提出了一种能够节省计算资源的比较算法,可以大幅提高软件计算spwm数据计算速度。 一、载波比与控制精度的关系 很多文章介绍了自然采样法的数学方法,并给出了各种优化算法,这些算法力图精确求解三角方程与正弦方程的交点,由于运算中带有大量的浮点运算若没有dsp 或高速浮点处理芯片的支持必然会造成运算时间过长对实时调控产生影响。实际上我们需要的计算精度和每载波周期可能的开关点数量有关系,此数值用C 来表示,称其为控制比(下文同)数值上=载波周期/pwm 周期,同步调制方式中此值为整数,可以理解为用多少个 pwm 周期控制一个载波周期。pwm 频率实际上是开关电路的极限频率或最理想工作的频率,假设每载波周期可能的开关点数量为512 个则需要二进制的9 位计算精度如果再加一位存疑位最多计算10 位就够了。如果采用数据类型 IEEE32 浮点数迭代运算将得到 24 位(二进制)精度的计算结果,与实际需要相差甚远。在这里特别指出计算精度与具体的数值大小无关。从另一个角度看由于 pwm 频率的限制有高精度的计算结果也无法实施高精度的开关控制。可以采用两种方法减少这种无意义的计算资源浪费第一种方法是在迭代算法中加入精度条件限制,这需要重新编写迭代函数、浮点库函数和三角运算库函数难度较大。第二种方法是采用基于数值比较的方法确定计算结果,下面就第二种方法展开讨论。 二、比较法基本思想 首先考虑锯齿波的计算。假设调制比 M=m1 载波比为整数N=n1 的pwm 数据已经计算完成, 图中虚线为可能的开关点位置,定义每项计算值 x 的数学含义为真值落入区间(x,x+1]之中,当 N 值不变时如果 m2>m1时可以确定每一项的计算值一定增大,那么我们只需从当前值+1 开始依次校验后面的开关点找到满足不等式 m2*sinxKx的最大 x 值。 图 1 M 值变大时计算值变大 y=...