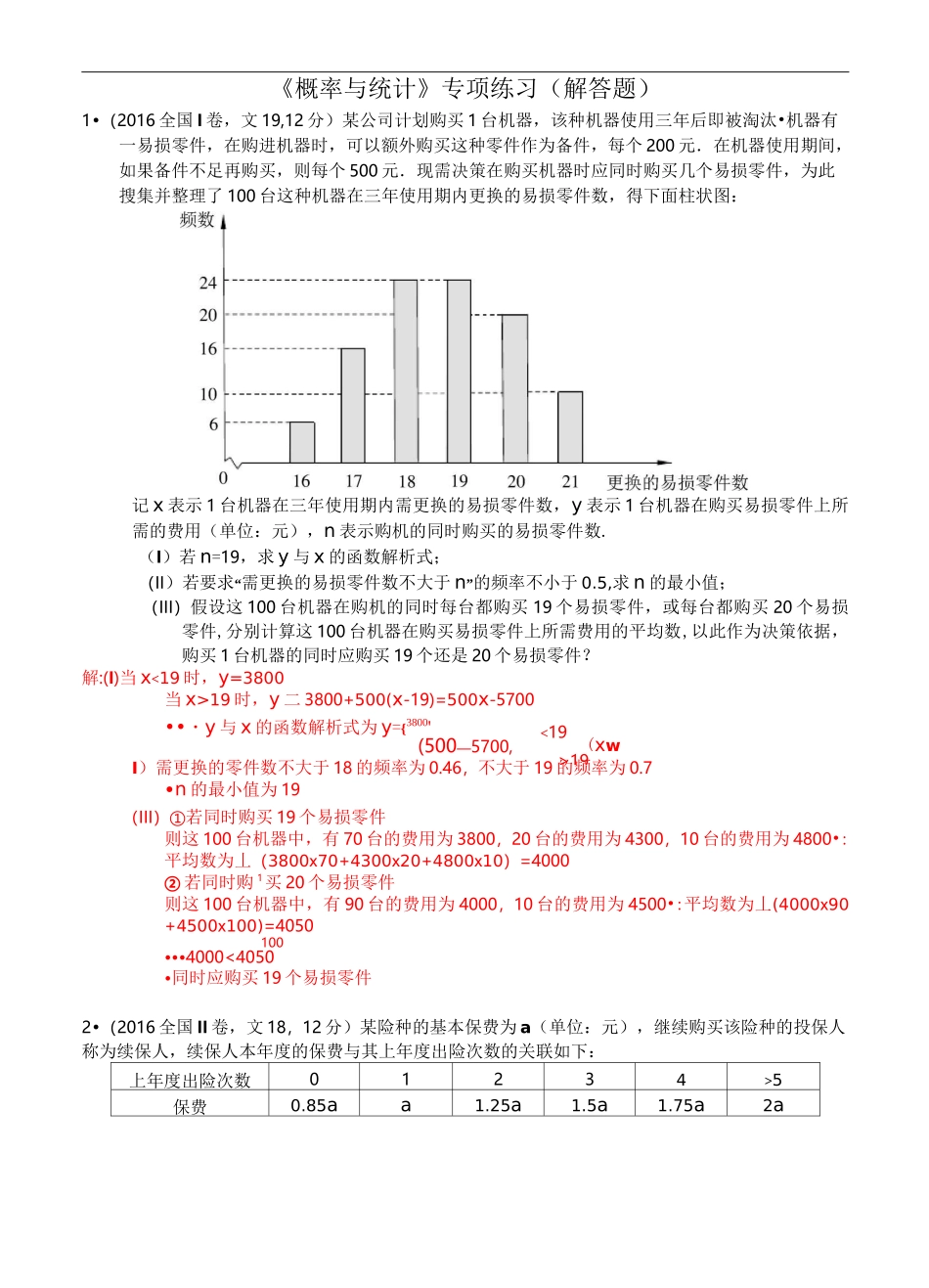
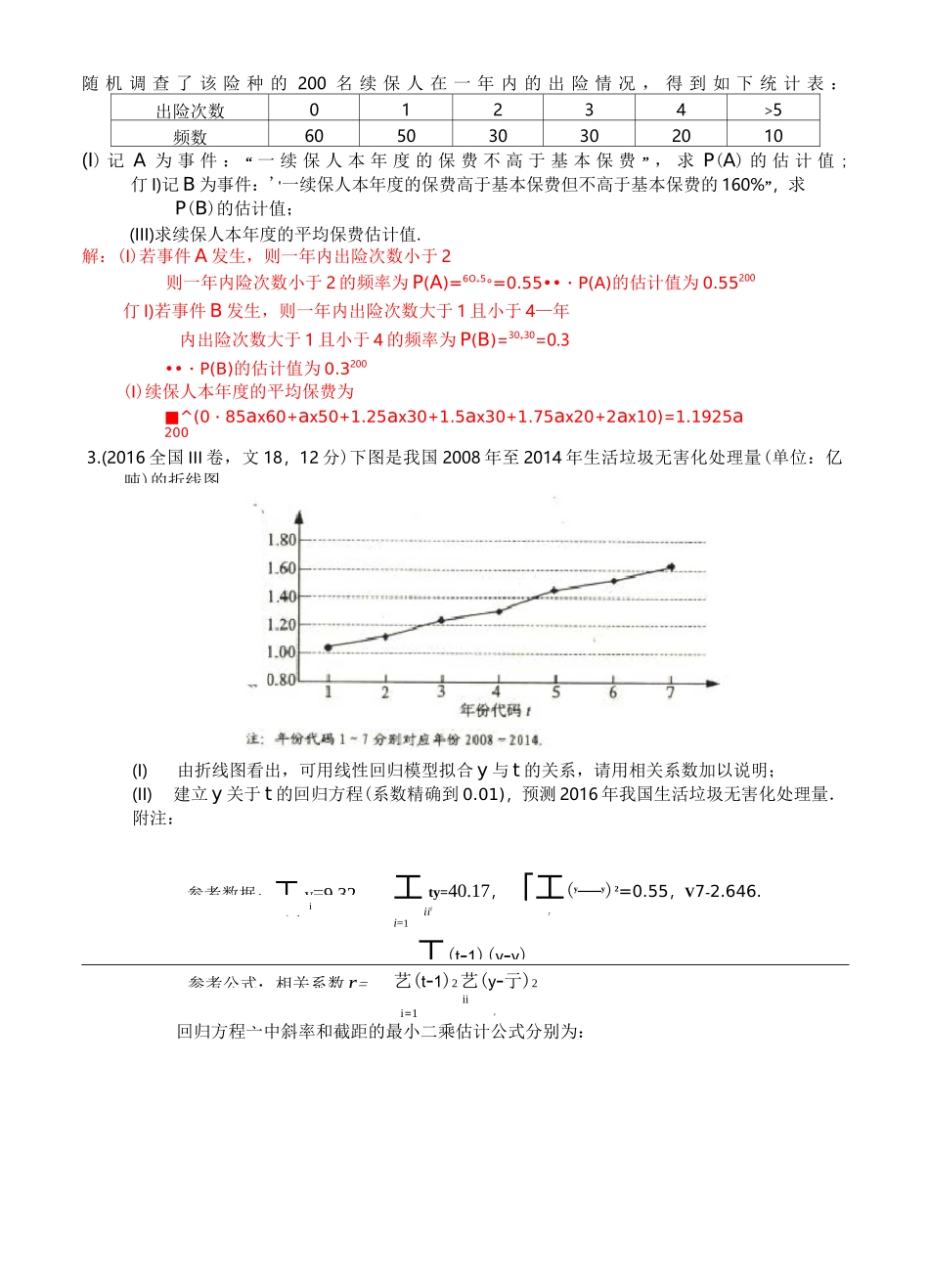
<19>19(xw《概率与统计》专项练习(解答题)1•(2016 全国 I 卷,文 19,12 分)某公司计划购买 1 台机器,该种机器使用三年后即被淘汰•机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个 200 元.在机器使用期间,如果备件不足再购买,则每个 500 元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了 100 台这种机器在三年使用期内更换的易损零件数,得下面柱状图:记 x 表示 1 台机器在三年使用期内需更换的易损零件数,y 表示 1 台机器在购买易损零件上所需的费用(单位:元),n 表示购机的同时购买的易损零件数.(I)若 n=19,求 y 与 x 的函数解析式;(II)若要求“需更换的易损零件数不大于 n”的频率不小于 0.5,求 n 的最小值;(III)假设这 100 台机器在购机的同时每台都购买 19 个易损零件,或每台都购买 20 个易损零件,分别计算这 100 台机器在购买易损零件上所需费用的平均数,以此作为决策依据,购买 1 台机器的同时应购买 19 个还是 20 个易损零件?解:(I)当 x<19 时,y=3800当 x>19 时,y 二 3800+500(x-19)=500x-5700••・y 与 x 的函数解析式为 y={3800'(500—5700,I)需更换的零件数不大于 18 的频率为 0.46,不大于 19 的频率为 0.7•n 的最小值为 19(III)①若同时购买 19 个易损零件则这 100 台机器中,有 70 台的费用为 3800,20 台的费用为 4300,10 台的费用为 4800•:平均数为丄(3800x70+4300x20+4800x10)=4000② 若同时购 1买 20 个易损零件则这 100 台机器中,有 90 台的费用为 4000,10 台的费用为 4500•:平均数为丄(4000x90+4500x100)=4050100•••4000<4050•同时应购买 19 个易损零件2•(2016 全国 II 卷,文 18,12 分)某险种的基本保费为 a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:上年度出险次数01234>5保费0.85aa1.25a1.5a1.75a2a参考数据:工 y=9.32,ii=1工 ty=40.17,「工(y—y)2=0.55,V7-2.646.iiii=1工(t-1)(y-y)i参考公式:相关系数 r=i随 机 调 查 了 该 险 种 的 200 名 续 保 人 在 一 年 内 的 出 险 情 况 , 得 到 如 下 统 计 表 :出险次数01234>5频数605030302010(I) 记 A 为 事 件 : “ 一 续 保 人 本 年 度 的 保 费 不 高 ...