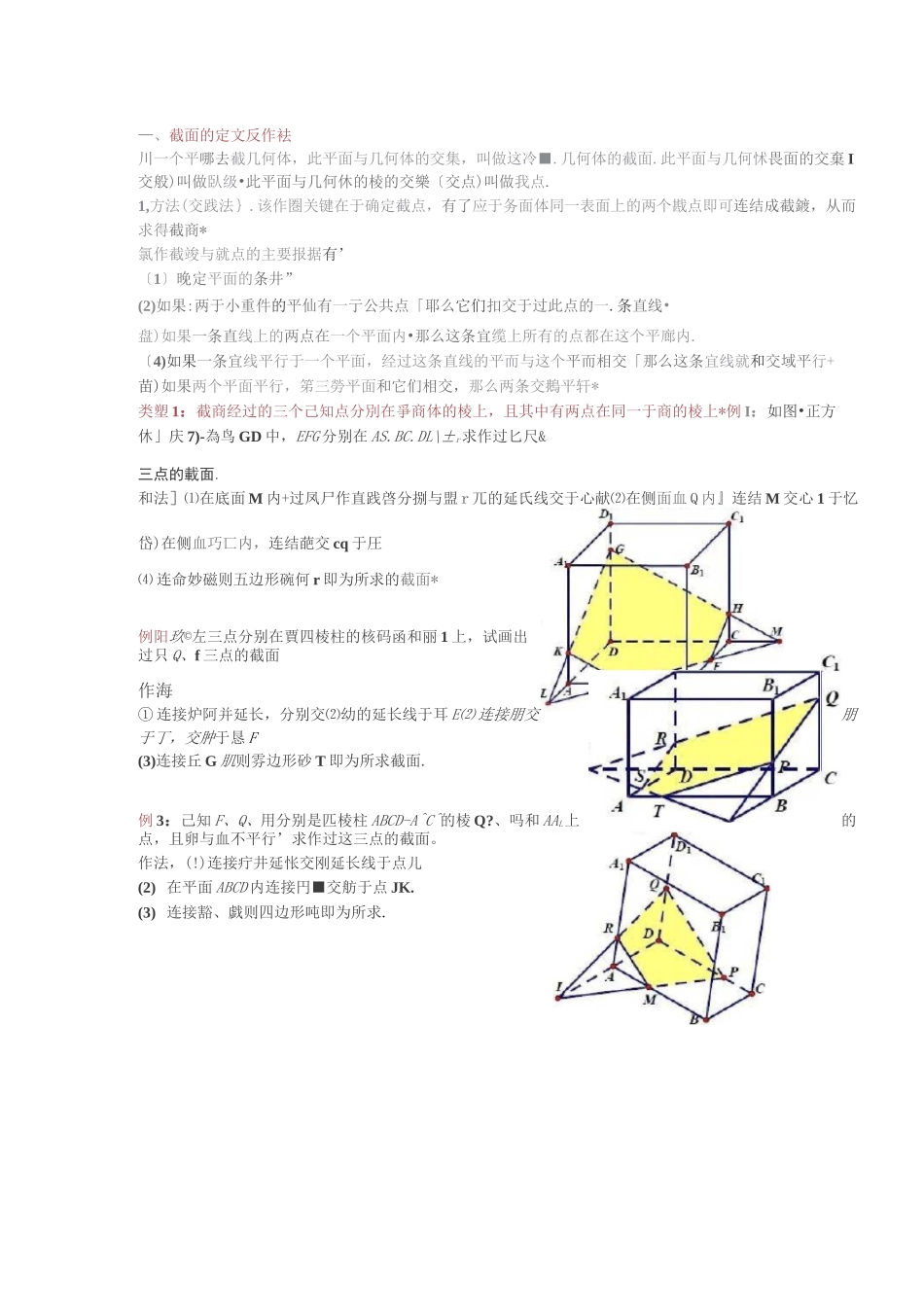
立体几何中的截面问题,一看就懂了例题几何中的截面问题—、截面的定文反作袪川一个平哪去截几何体,此平面与几何体的交集,叫做这冷■.几何体的截面.此平面与几何怵畏面的交棄 I交般)叫做臥级•此平面与几何休的棱的交樂〔交点)叫做我点.1,方法(交践法}.该作圏关键在于确定截点,有了应于务面体同一表面上的两个戡点即可连结成截鍍,从而求得截商*氯作截竣与就点的主要报据有’〔1〕晚定平面的条井”(2)如果:两于小重件的平仙有一亍公共点「耶么它们扣交于过此点的一.条直线•盘)如果一条直线上的两点在一个平面内•那么这条宜缆上所有的点都在这个平廊内.〔4)如果一条宜线平行于一个平面,经过这条直线的平而与这个平而相交「那么这条宜线就和交域平行+苗)如果两个平面平行,笫三勞平面和它们相交,那么两条交鵝平轩*类塑 1:截商经过的三个己知点分別在爭商体的棱上,且其中有两点在同一于商的棱上*例 I:如图•正方休」庆 7)-為鸟 GD 中,EFG 分别在 AS.BC.DL\±r求作过匕尺&三点的載面.和法]⑴在底面 M 内+过凤尸作直践啓分捌与盟 r 兀的延氏线交于心献⑵在侧面血 Q 内』连结 M 交心 1 于忆岱)在侧血巧匸内,连结葩交 cq 于圧⑷ 连命妙磁则五边形碗何 r 即为所求的截面*例阳玖©左三点分别在賈四棱柱的核码函和丽 1 上,试画出过只 Q、f 三点的截面作海① 连接炉阿并延长,分别交⑵幼的延长线于耳 E⑵ 连接朋交朋于丁,交肿于恳 F(3)连接丘 G 肌则雰边形砂 T 即为所求截面.例 3:己知 F、Q、用分别是匹棱柱 ABCD-A^C^的棱 Q?、吗和 AAL上的点,且卵与血不平行’求作过这三点的截面。作法,(!)连接疔井延怅交刚延长线于点儿(2) 在平面 ABCD 内连接円■交舫于点 JK.(3) 连接豁、戯则四边形吨即为所求.拥丟如图,正方体個⑦一如址 q 坷中,E、尸在两条棱上,&在底面九勺内,求过忒玖旷的截面.变坷勺干点畑则面/钙坷为所作的辅助面.例 4*如图,五棱锥产-如朋中,三条侧棱丄各有一己知点 F、G&求作过只從捉的截面.柞法:(1)将侧面冈圧 PBC.磁忡展得到三棱雜 P-SST.(刃在侧而加内,连结井延长飯兗刖于尺(引在侧面丹丁内,连结并延长覘交砂干匸⑷在侧面用亍内,连结皿分别交PD、FE 予忒&⑸ 连结丹;姐则五边形翊£V 即为所求的截面类型 2:截面经过时三个已知成至少有一点在多面体的面上,其余点在樓上跖作法:<1)itK 尸作辅助面,在面$勺内,过尸作叭卩叭⑵ 在面個内,延长巧如交睦的...