2025年28.浙江省数学竞赛模拟题答案

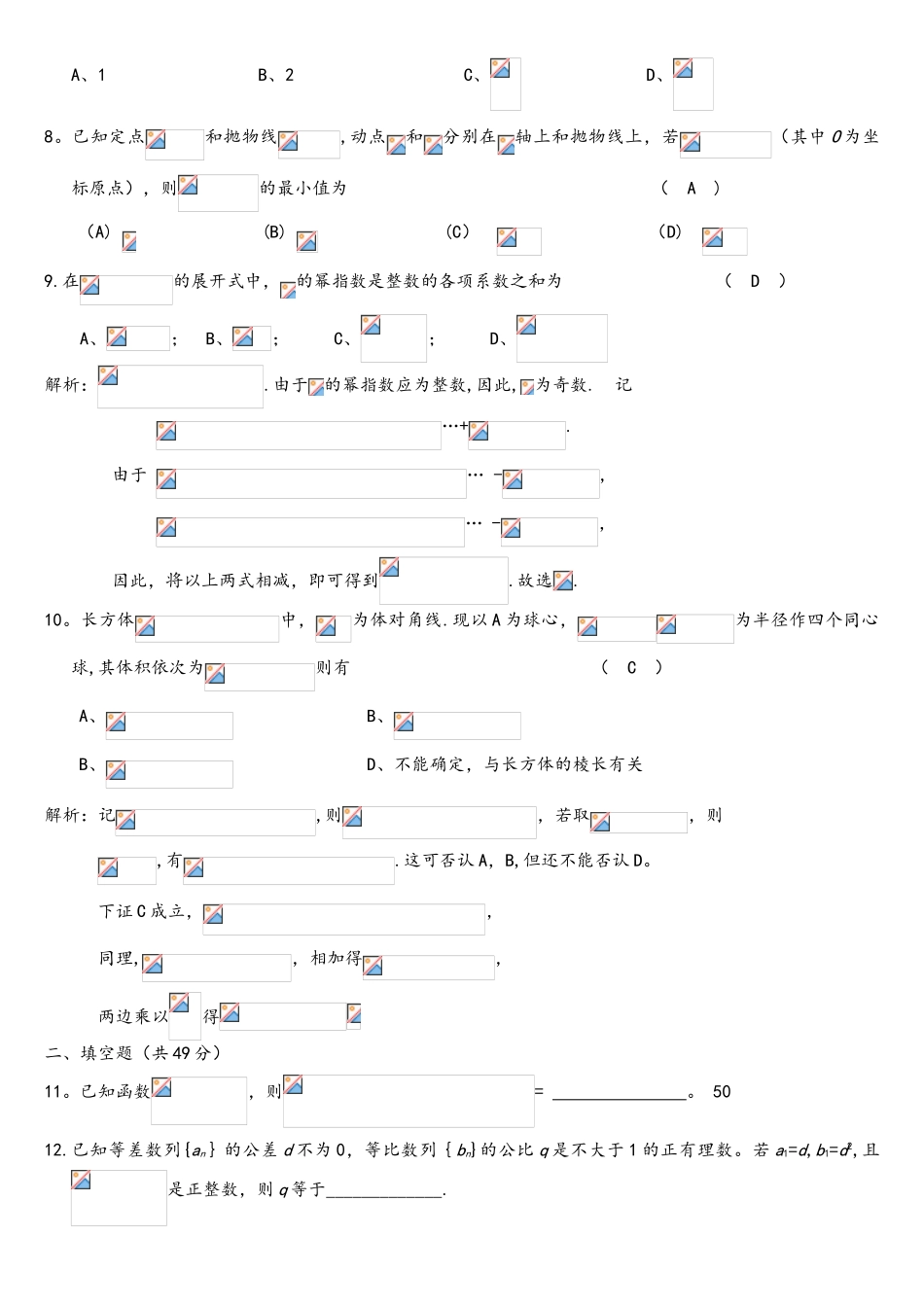
浙江省数学竞赛模拟题（十四)班级__________ 姓名__________一、选择题(共 50 分）1.已知，定义，则A． B． C． D． （ C )解：计算可知是最小正周期为６的函数。即得,因此＝2。设锐角使有关 x 的方程有重根,则的弧度数为 （ B ）A． B． C． D． 解：因方程有重根,故 得，于是。 故选 B.3。已知直线与圆R 有交点， 则 的最小值是 （ B ）A． B． C． D．4。已知函数,则 （ C ）A．1 B．0 C． —1 D．45。记，，则＝ （ C ） (A) （B) (C) (D) 6。平面直角坐标系中,横、纵坐标都是整数的点称为整点。那么满足不等式的整点的个数为 ( A ） A、16 B、17 C、18 D、257。设都是正数，则的最大值为 （ C ）A、1 B、2 C、 D、8。已知定点和抛物线,动点和分别在轴上和抛物线上，若（其中 O 为坐标原点），则的最小值为 （ A ) （A) (B) (C） （D) 9.在的展开式中，的幂指数是整数的各项系数之和为 （ D ）A、； B、； C、； D、解析：.由于的幂指数应为整数,因此, 为奇数. 记 …+. 由于 … -, … -， 因此，将以上两式相减，即可得到.故选.10。长方体中，为体对角线.现以 A 为球心，为半径作四个同心球,其体积依次为则有 （ C ）A、 B、B、 D、不能确定，与长方体的棱长有关解析：记,则，若取，则,有.这可否认 A，B,但还不能否认 D。下证 C 成立，，同理,，相加得，两边乘以得二、填空题（共 49 分）11。已知函数，则= 。 5012.已知等差数列{an｝的公差 d 不为 0，等比数列｛bn}的公比 q 是不大于 1 的正有理数。若 a1=d,b1=d2,且是正整数，则 q 等于_____________.解析:由于，故由已知条件懂得：1+q+q2 为，其中 m为正整数。令,则。由于 q 是不大于 1 的正有理数,因此,即 5≤m≤13 且是某个有理数的平方,由此可知。13。函数（，其中为正整数）的值域中共有个整数，则正整数 。 100314.函数的值域为 .15.方程的解为____________________。16.设，则的最小值是______________.17。已知函数R →R 满足：对任意R ，均有，则所有满足条件的函数 f 为 ．三、解答题（共 51 分）18.设三边长分别为,且。求的最小值.解：==由于是三边长，且，因此 ， 于是，即∴。等号当且仅当时取到，故的最小值为。19.已知在数列中,，(R，R 且0，N ）。 （1）若数列是等比数列，求与满足的条件；（2)当，时，一种质点在平面直...