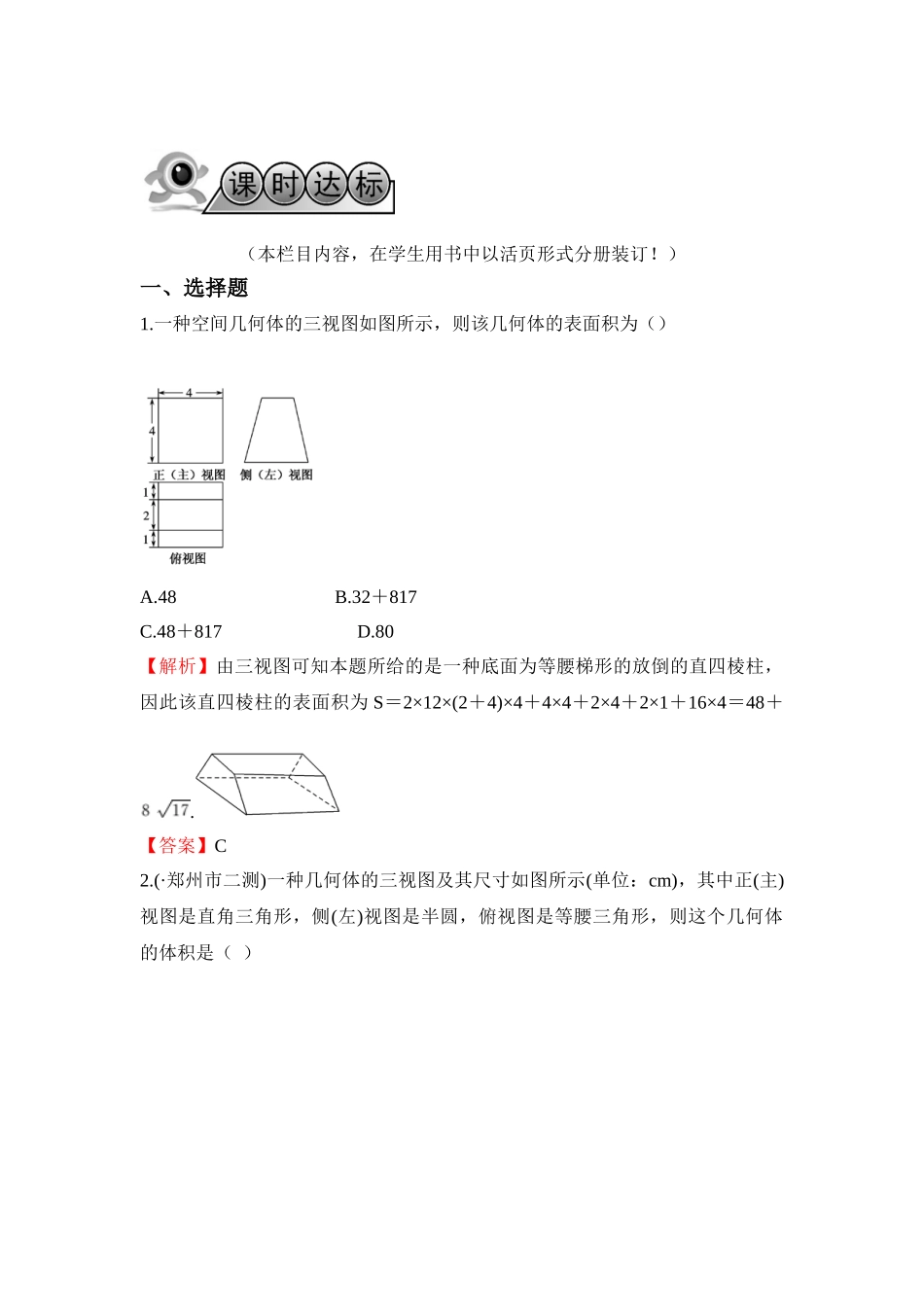
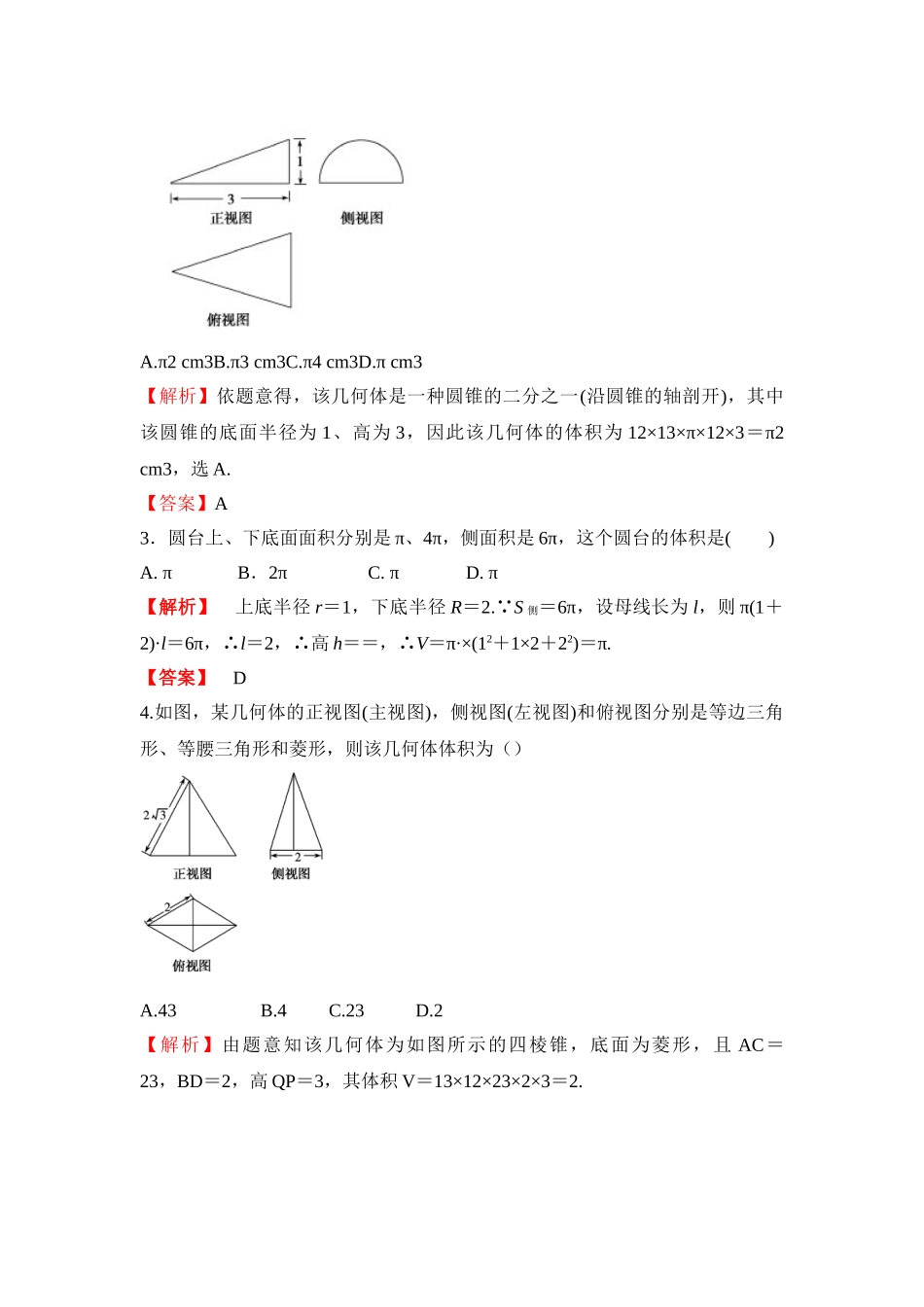
(本栏目内容,在学生用书中以活页形式分册装订!)一、选择题1.一种空间几何体的三视图如图所示,则该几何体的表面积为()A.48 B.32+817C.48+817 D.80【解析】由三视图可知本题所给的是一种底面为等腰梯形的放倒的直四棱柱,因此该直四棱柱的表面积为 S=2×12×(2+4)×4+4×4+2×4+2×1+16×4=48+.【答案】C2.(·郑州市二测)一种几何体的三视图及其尺寸如图所示(单位:cm),其中正(主)视图是直角三角形,侧(左)视图是半圆,俯视图是等腰三角形,则这个几何体的体积是( )A.π2 cm3B.π3 cm3C.π4 cm3D.π cm3【解析】依题意得,该几何体是一种圆锥的二分之一(沿圆锥的轴剖开),其中该圆锥的底面半径为 1、高为 3,因此该几何体的体积为 12×13×π×12×3=π2 cm3,选 A.【答案】A3.圆台上、下底面面积分别是 π、4π,侧面积是 6π,这个圆台的体积是( )A. πB.2πC. πD. π【解析】 上底半径 r=1,下底半径 R=2. S 侧=6π,设母线长为 l,则 π(1+2)·l=6π,∴l=2,∴高 h==,∴V=π·×(12+1×2+22)=π.【答案】 D4.如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等边三角形、等腰三角形和菱形,则该几何体体积为()A.43 B.4 C.23 D.2【解析】由题意知该几何体为如图所示的四棱锥,底面为菱形,且 AC=23,BD=2,高 QP=3,其体积 V=13×12×23×2×3=2.【答案】C5.已知正四面体 ABCD 的表面积为 S,其四个面的中心分别为 E、F、G、H,设四面体 EFGH 的表面积为 T,则 TS 等于()A.19 B.49 C.14 D.13【解析】设正四面体 ABCD 的棱长为 a,如图所示,则 EF=23MN=13BD=13a,因此 TS=19.【答案】A6.已知正三棱柱内接于一种半径为 2 的球,则正三棱柱的侧面积获得最大值时,其底面边长为( )【解析】在如图所示的正三棱柱 A1B1C1ABC 中,设底面边长为 a,其高 SE=h,O 为其外接球的球心.在 Rt△OAE 中,OA=R,OE=h2,,∴OA2=OE2+AE2,二、填空题7. 如图所示,三棱柱 ABC-A1B1C1的所有棱长均为 a,∠A1AB=∠A1AC=60°,则其全面积为_____.【解析】如图,过 B 作 BD⊥AA1 于 D,连接 CD,则△BAD≌△CAD,∴∠ADB=∠ADC=90°,∴AD⊥CD,AD⊥BD,∴△BCD 为垂直于侧棱 AA1的截面.又 ∠BAD=60°,AB=a,∴BD=32a.∴△BDC 的周长为()a,从而 S 侧=,【答案】8.如图,半径为 4 的球 O 中有一内接...