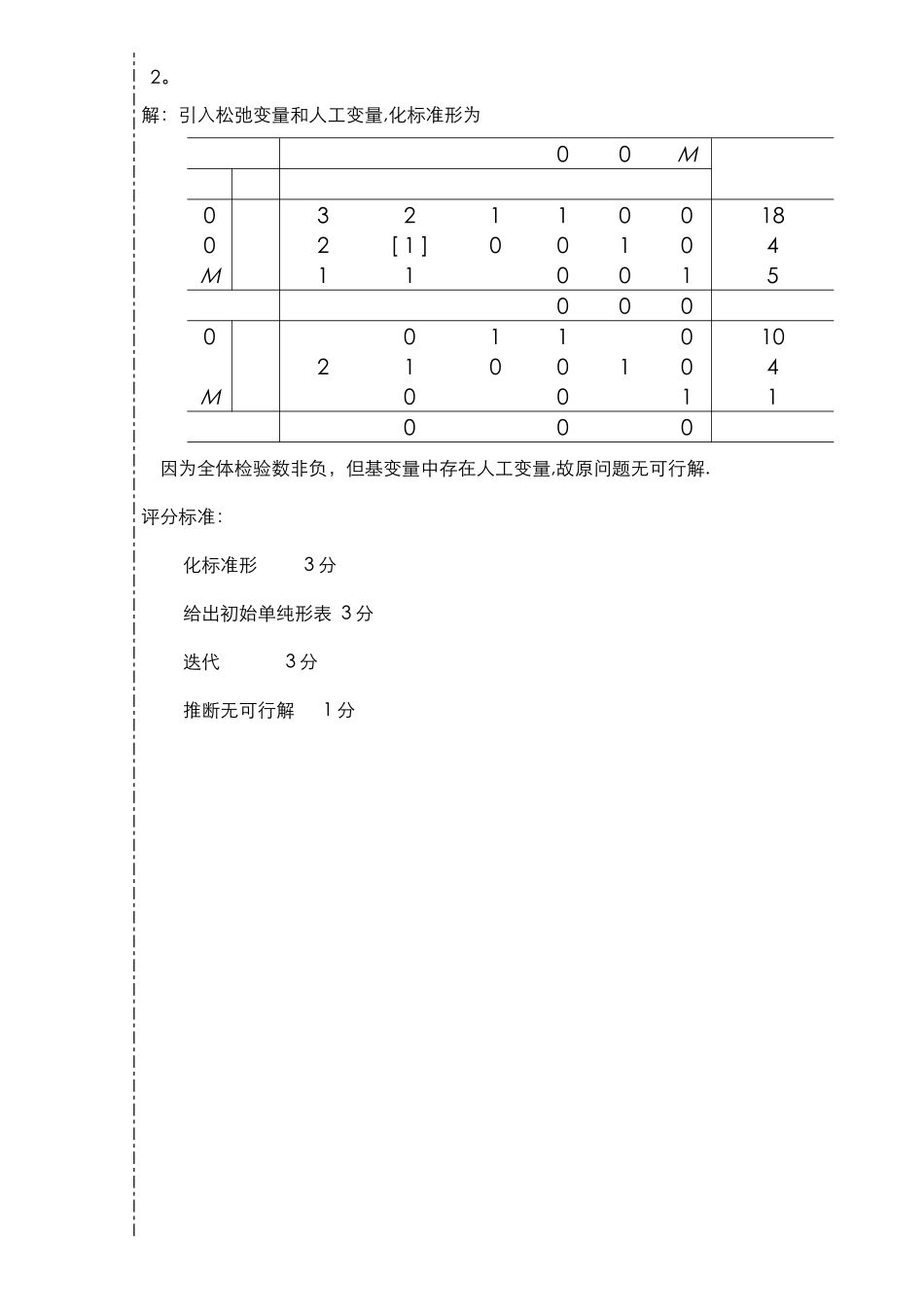
五邑大学试卷答案及评分标准 试卷分类(A 卷或 B 卷) A 学期: 2024 至 2024 学年度 第 2 学期 课程: 管理运筹学 专业: 信管、电子商务、市场营销 班级学号: 姓名: 一、 求解下述线性规划问题(共 30 分,每小题 10 分)1. 解: (1) 画直角坐标系……………………………………1 分(2) 画约束条件,决定可行域………………………5 分(3) 画目标函数线……………………………………7 分(4) 移动目标函数线,得到最优解…………………10 分得分2。 解:引入松弛变量和人工变量,化标准形为00M03211001802[ 1 ]00104M11001500000110102100104M0011000 因为全体检验数非负,但基变量中存在人工变量,故原问题无可行解.评分标准: 化标准形 3 分 给出初始单纯形表 3 分 迭代 3 分 推断无可行解 1 分3. 解:31111[2]10413101620011021[4]0140010由上表得到最优解,因存在非基变量的检验数为 0,故本题具有无穷多解.评分标准:初始单纯形表 4 分; 得到最优解 5 分; 推断存在无穷多最优解 1 分。二、 已知如下产销量及运价表,求解此运输问题(20 分)产销量及运价表解:(1)由伏格尔法求初始调运方案产销平衡表单位运价表(2)用位势法求检验数检验数表(3)因为全体检验数非负,所以初始调运方案即为最优解.评分标准:求初始调运方案 9 分求检验数 9 分推断最优解 2 分得分三、 用隐枚举法求解下述 0—1 规划问题(15 分)解:第一步,将上述线性规划问题转换成法律规范形式(1)目标函数求微小化,约束条件为“”形式 ……………………………。.2 分(2)令, ……………………………。。4 分(3)按目标函数变量系数的大小从小到大排列变量,约束条件也作相应的调整 …………………………….。6 分 第二步,检验全零解,不是可行解. ……………………………。。8 分 第三步,依次分枝,直到得到最优解。 本问题的最优解为, …………………………….。15 分得分四、 求解下述标准指派问题(10 分) 四人完成四项工作,他们完成各项任务的时间(小时)如下表所示,如何安排四人的工作,才能使完成这四项工作总的时间消耗最少。解:指派方案为:人员 1→工作 4;人员 2→工作 1;人员 3→工作 3;人员 4→工作 2消耗的最小时间为:43评分标准:第一个矩阵 3 分;第二个矩阵 5 分;给出最优解 2 分。得分五、 用动态规划求解下述非线性问题(15 分)解...