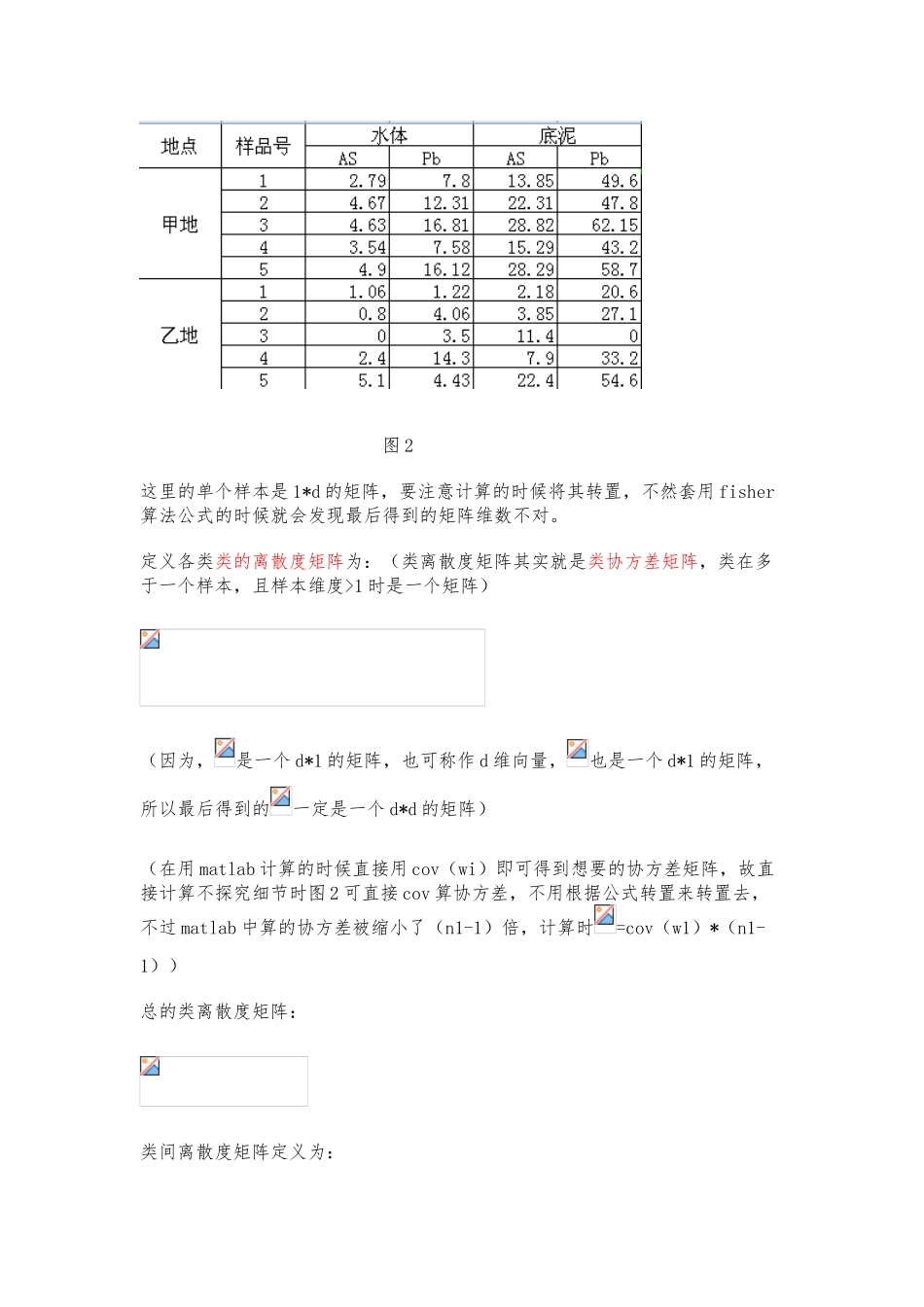
Fisher 判别法讲解以与 matlab 代码实现两类的线形判别问题可以看作是把所有样本都投影到一个方向上,然后在这个一维空间中确定一个分类的阈值。过这个预置点且与投影方向垂直的超平面就是两类的分类面。第一个问题,如何确定投影方向?这里只讨论两类分类的问题.训练样本集是 X={x1,x2...xn},每个样本是一个 d维向量,其中第一类 w1={,...},第二类 w2={,...}。我们要寻求一个投影方向 w(w 也是一个 d 维向量),投影以后样本变成:=(y 是一个标量),i=1...n在原样本空间中,类均值为: i=1,2(一共两类的均值)(ps.是一个 d*1 的矩阵,假设每个维度是一个变量值,mi 中的每一维度就是这些变量值的均值,如以下图所示: 图 1特别注明:有些例子给的矩阵是这样的: 图 2这里的单个样本是 1*d 的矩阵,要注意计算的时候将其转置,不然套用 fisher算法公式的时候就会发现最后得到的矩阵维数不对。定义各类类的离散度矩阵为:(类离散度矩阵其实就是类协方差矩阵,类在多于一个样本,且样本维度>1 时是一个矩阵)(因为,是一个 d*1 的矩阵,也可称作 d 维向量,也是一个 d*1 的矩阵,所以最后得到的一定是一个 d*d 的矩阵)(在用 matlab 计算的时候直接用 cov(wi)即可得到想要的协方差矩阵,故直接计算不探究细节时图 2 可直接 cov 算协方差,不用根据公式转置来转置去,不过 matlab 中算的协方差被缩小了(n1-1)倍,计算时=cov(w1)*(n1-1))总的类离散度矩阵:类间离散度矩阵定义为:在投影以后的一维空间里,两类的均值分别是; i=1,2故类离散度不再是一个矩阵,而是一个值 i=1,2总类离散度为:类间离散度:要使得需求的方向投影能在投影后两类能尽可能的分开,而各类部又尽可能的聚集,可表示成如下准则,即 fisher 准则:将公式代入并通过拉格朗日求极值的方法,可得投影方向:(w 是一个 d*1 的矩阵,或者说亦是一个 d 维向量)阈值可表示为:最后将待确定样本代入推断的符号和哪个类相同,确定其属于哪个类别。例子(注意表格中所给的样本维度和公式中变量维度的问题)代码已经运行无误代码:%读取excel中特定单元格的数据w12=xlsread('E:\模式识别\理论学习\胃病分类问题.xls','C2:F16');%分别选取类1和类2、测试样本的数据w1=w12(1:5,:);w2=w12(6:12,:);sample=w12(13:15,:);%计算类1和类2的样本数r1=size(w1,1);r2=size(w2,1);r3=size(sample,1);%计算类1和类2的均值(矩阵)m1...