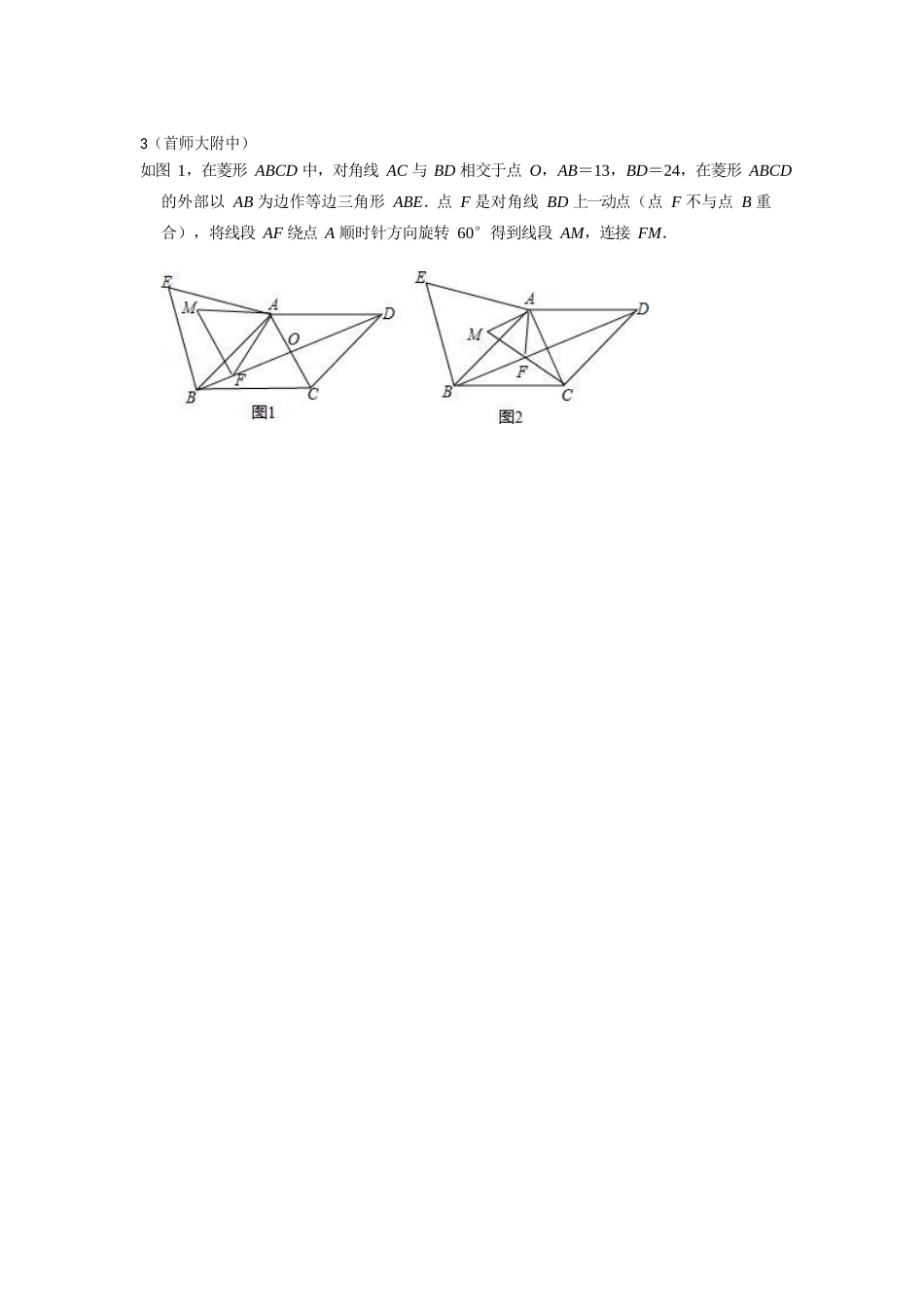
1(人大附)2(清华附中)3(首师大附中)如图 1,在菱形 ABCD 中,对角线 AC 与 BD 相交于点 O,AB=13,BD=24,在菱形 ABCD 的外部以 AB 为边作等边三角形 ABE.点 F 是对角线 BD 上一动点(点 F 不与点 B 重合),将线段 AF 绕点 A 顺时针方向旋转 60°得到线段 AM,连接 FM.4(101 中学)在△ABC 中,∠C=90°,AC=BC,点 D 在射线 BC 上(不与点 B、C 重合),连接 AD,将 AD 绕点 D 顺时针旋转 90°得到 DE,连接 BE.(1)如图 1,点 D 在 BC 边上.① 依题意补全图 1;② 作 DF⊥BC 交 AB 于点 F,若 AC=8,DF=3,求 BE 的长;(2)如图 2,点 D 在 BC 边的延长线上,用等式表示线段 AB、BD、BE 之间的数量关系(直接写出结论).证明吗?5(师达中学)已知正方形 ABCD,点 E、F 分别在射线 AB、射线 BC 上, AE BF ,DE 与 AF 交于点 O.(1)如图 1,当点 E、F 分别在射向 AB、BC 上时,则线段 DE 于 AF 的数量关系是 ,位置关系是 .(2)如图 2,当点 E 在线段 AB 延长线上时,将线段 AE 沿 AF 进行平移至 FG,连接 DG.① 依题意将图 2 补全;② 在点 E 运动的过程中,DG、AD、AE 之间始终保持一种等量关系,你能找到这个关系并6(海淀外国语)7(十一学校)如图 1,在△ABC 中,∠ACB=90°,AC=BC,E 为∠ACB 平分线 CD 上一动点(不与点 C 重合),点 E 关于直线 BC 的对称点为 F,连接 AE 并延长交 CB 延长线于点 H,连接 FB 并延长交直线 AH 于点 G.(1)求证:AE=BF.(2)用等式表示线段 FG,EG 与 CE 的数量关系,并证明.(3)连接 GC,用等式表示线段 GE,GC 与 GF 的数量关系是 .8(四中)1. 如图①,在等腰 Rt△ABC 中,∠ACB=90°,CD 平分∠ACB 交 AB 于点 D.点 P 为线段 CD 上一点(不与端点 C,D 重合),PE⊥PA,PE 与 BC 的延长线交于点 E,与 AC 交于点 F,连接 AE,AP,BP.(1)求证:AP=BP;(2)求∠EAP 的度数;(3)探究线段 EC,PD 之间的数量关系,并证明.图①备用图9(八中)10(北师大附属实验中学)11(陈经纶望京实验中学)12(海淀实验中学)13(交大附中)14(十八中)15(科大附中)16(五中分校)17(育鸿学校)218(东直门中学)26.四边形 ABCD 是正方形,△BEF 是等腰直角三角形,∠BEF=90°,BE=EF,连接...