常见辅助线的作法有以下几种

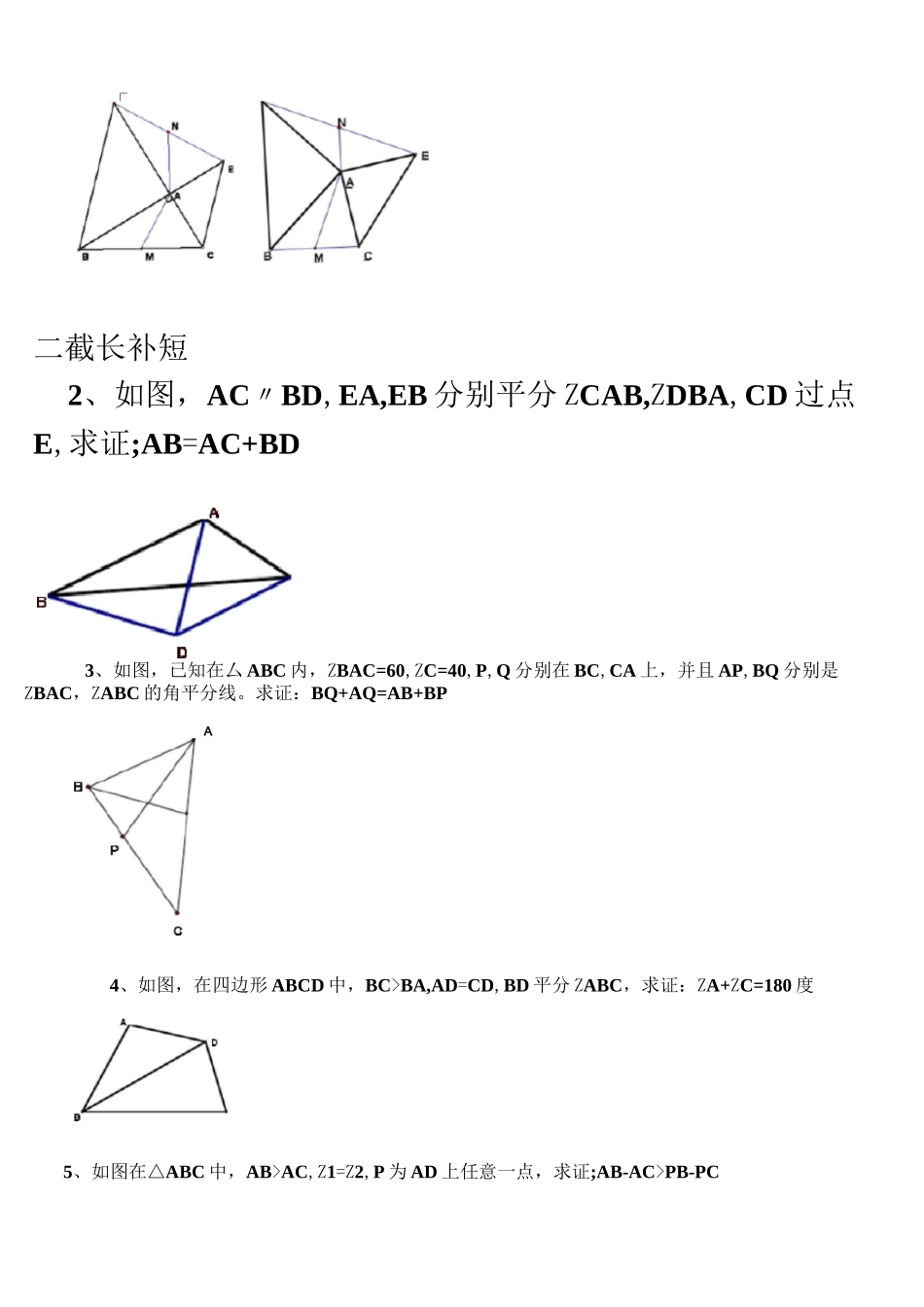
常见辅助线的作法有以下几种常见辅助线的作法有以下几种：1）遇到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思维模式是全等变换中的“对折”.2）遇到三角形的中线，倍长中线，使延长线段与原中线长相等，构造全等三角形，利用的思维模式是全等变换中的“旋转”.3）遇到角平分线，可以自角平分线上的某一点向角的两边作垂线，利用的思维模式是三角形全等变换中的“对折”，所考知识点常常是角平分线的性质定理或逆定理.4）过图形上某一点作特定的平分线，构造全等三角形，利用的思维模式是全等变换中的“平移”或“翻转折叠”5）截长法与补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，是之与特定线段相等，再利用三角形全等的有关性质加以说明.这种作法，适合于证明线段的和、差、倍、分等类的题目.特殊方法：在求有关三角形的定值一类的问题时，常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答.一、倍长中线（线段）造全等例 1、（“希望杯”试题）已知，如图△ABC 中，AB=5,AC=3，则中线 AD 的取值范围是,例 2、如图，AABC 中，E、F 分别在 AB、AC 上,DE 丄 DF,D 是中点，试比较 BE+CF 与 EF 的大小.例 3、如图，AABC 中，BD=DC=AC，E 是 DC 的中点，求证：AD 平分 ZBAE.应用：1、（09 崇文二模）以厶 ABC 的两边 AB、AC 为腰分别向外作等腰 Rt^ABD 和等腰Rt^ACE，ZBAD=ZCAE=90，连接 DE，M、N 分别是 BC、DE 的中点.探究：AM 与 DE 的位置关系及数量关系.（1）如图①当厶 ABC 为直角三角形时，AM 与 DE 的位置关系是，线段 AM 与 DE 的数量关系是；（2）将图①中的等腰 Rt^ABD 绕点 A 沿逆时针方向旋转 0（0<0<90）后，如图②所示，（1）问中得到的两个结论是否发生改变？并说明理由.二截长补短2、如图，AC〃BD,EA,EB 分别平分 ZCAB,ZDBA,CD 过点E,求证;AB=AC+BD3、如图，已知在厶 ABC 内，ZBAC=60,ZC=40,P,Q 分别在 BC,CA 上，并且 AP,BQ 分别是ZBAC，ZABC 的角平分线。求证：BQ+AQ=AB+BPA4、如图，在四边形 ABCD 中，BC>BA,AD=CD,BD 平分 ZABC，求证：ZA+ZC=180 度5、如图在△ABC 中，AB>AC,Z1=Z2,P 为 AD 上任意一点，求证;AB-AC>PB-PC□A应用：如图"在恥边形刖仞中”0"肚,点虚 SUE 上一个动恵’若£虑里 60 人初 2 处・且乙磁二那判断 AF）卜血与 BC 的关系并圧剧你洞站強■解:二、...