广东省佛山市顺德区均安中学2014高二数学 导数的几何意义导学案 新人教A版VIP专享

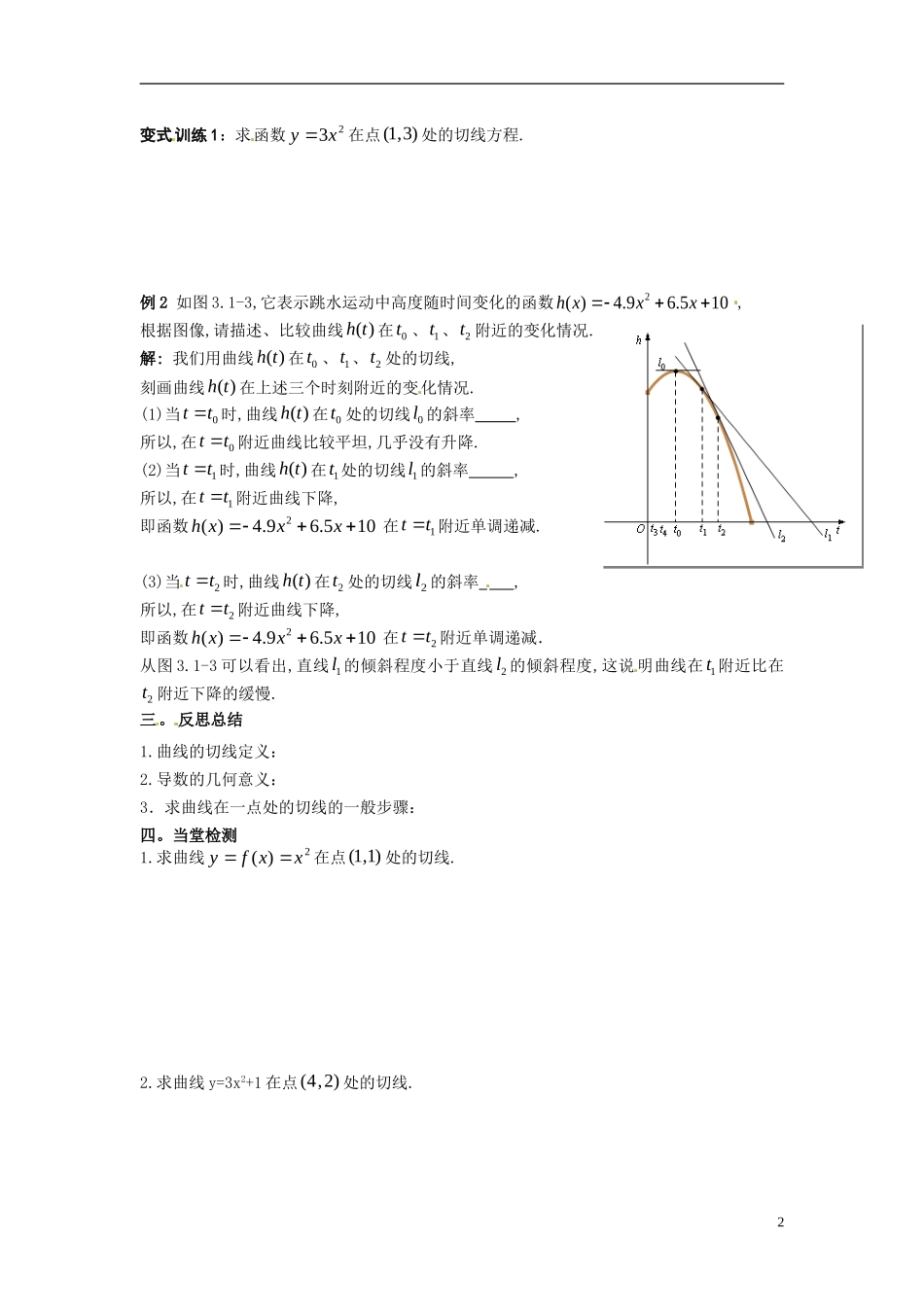
广东省佛山市顺德区均安中学 2014 高二数学 导数的几何意义导学案 新人教 A 版一．预习目标1.了解平均变化率与割线斜率之间的关系;2.理解曲线的切线的概念;3.通过函数的图像直观地理解导数的几何意义,并会用导数的几何意义解题。二．预习内容1.曲线的切线及切线的斜率（1）如图 3.1-2,当(,())(1,2,3,4)nnnP xf xn 沿着曲线( )f x 趋近于点00(,())P xf x时,即0x时 , 割 线nPP 趋 近 于 确 定 的 位 置 , 这 个 确 定 位 置 的 直 线 PT 称 为 .（2）割线nPP 的斜率是00()()nnnf xf xkxx,当点nP 沿着曲线无限接近点 P 时,nk 无限趋近于切线 PT 的斜率k ,即k = _________= 2.导数的几何意义函数)(xfy 在0xx 处的导数等于在该点00(,())xf x处的切线的斜率,即0()fx= . 说明: (1)当0x时,割线 PQ 的斜率,称为曲线在点 P 处的切线的斜率.这个概念: ① 提供了求曲线上某点切线的斜率的一种方法;② 切线斜率的本质—函数在0xx处的导数.(2)曲线在某点处的切线:1)与该点的位置有关;2)要根据割线是否有极限位置来判断与求解.如有极限,则在此点有切线,且切线是唯一的;如不存在,则在此点处无切线;3)曲线的切线,并不一定与曲线只有一个交点,可以有多个,甚至可以无穷多.三．提出疑惑同学们，通过你的自主学习，你还有哪些疑惑:课内探究学案（一）、合作探究1.导数的几何意义（1）函数)(xfy 在0xx 处的导数的几何意义是什么？__________________________（2）将上述意义用数学式表达出来。_________________________________________（3）根据导数的几何意义如何求曲线在某点处的切线方程？2.导函数（1）由函数)(xfy 在0xx 处求导数的过程可以看到,当0xx 时,0()fx是一个确定的数,那么,当 x 变化时, ( )fx便是 x 的一个函数,我们叫它为)(xf的导函数. 注: 在不致发生混淆时,导函数也简称导数.（二）。例题精析例 1 求曲线1)(2 xxfy在点)2,1(P处的切线方程.1变式训练 1：求函数23xy 在点(1,3) 处的切线方程.例 2 如图 3.1-3,它表示跳水运动中高度随时间变化的函数2( )4.96.510h xxx,根据图像,请描述、比较曲线 ( )h t 在 0t 、 1t 、 2t 附近的变化情况.解: 我们用曲线 ( )h t 在 0t 、 1t 、 2t 处的切线,刻画曲线 ( )h t 在上述三个时刻附近的变化情况.(1)当0tt时,曲线 ( )h t 在...