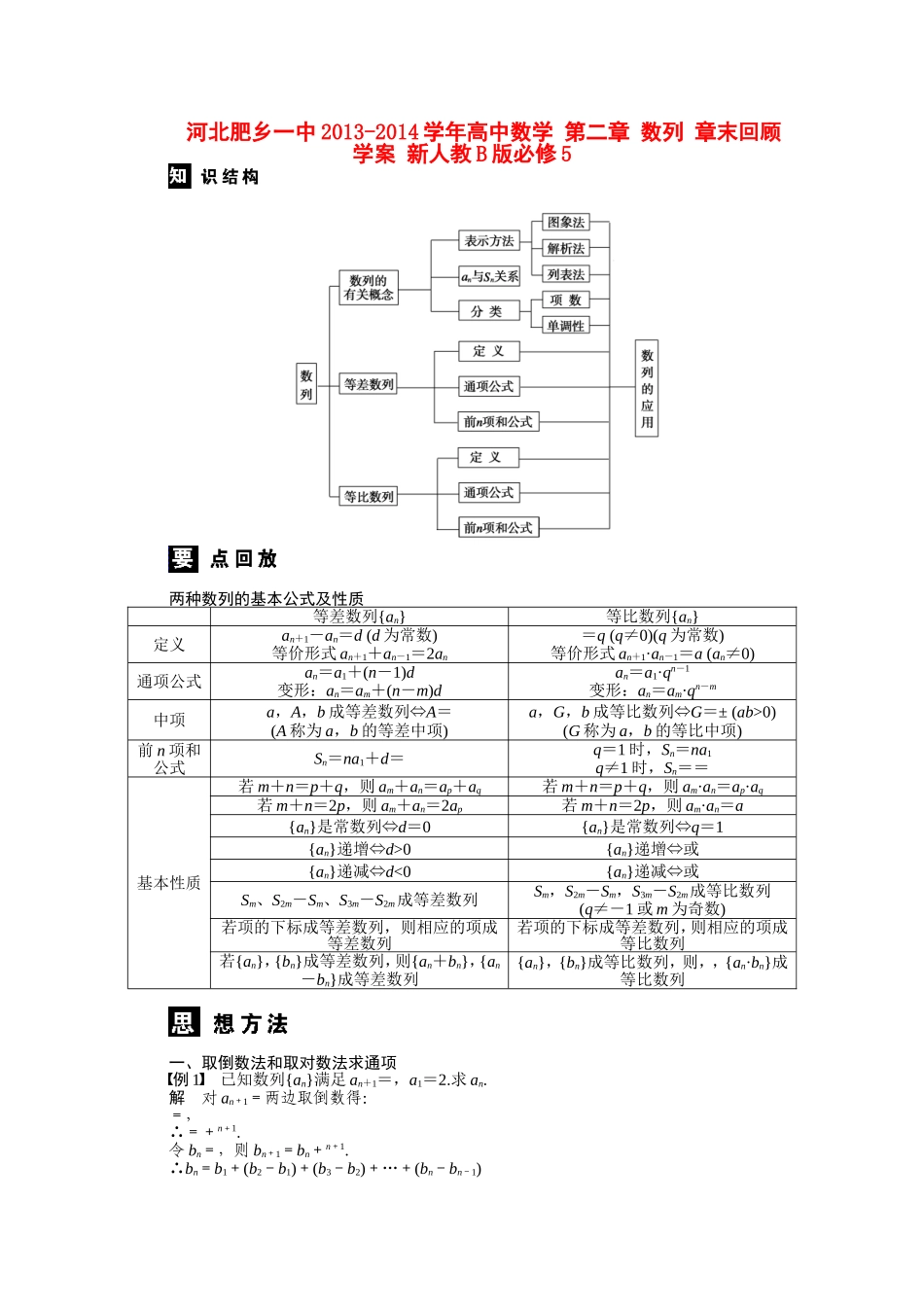
河北肥乡一中 2013-2014 学年高中数学 第二章 数列 章末回顾学案 新人教 B 版必修 5两种数列的基本公式及性质等差数列{an}等比数列{an}定义an+1-an=d (d 为常数) 等价形式 an+1+an-1=2an=q (q≠0)(q 为常数)等价形式 an+1·an-1=a (an≠0)通项公式an=a1+(n-1)d变形:an=am+(n-m)dan=a1·qn-1变形:an=am·qn-m中项a,A,b 成等差数列⇔A=(A 称为 a,b 的等差中项)a,G,b 成等比数列⇔G=± (ab>0)(G 称为 a,b 的等比中项)前 n 项和公式Sn=na1+d=q=1 时,Sn=na1q≠1 时,Sn==基本性质若 m+n=p+q,则 am+an=ap+aq若 m+n=p+q,则 am·an=ap·aq若 m+n=2p,则 am+an=2ap若 m+n=2p,则 am·an=a{an}是常数列⇔d=0{an}是常数列⇔q=1{an}递增⇔d>0{an}递增⇔或{an}递减⇔d<0{an}递减⇔或Sm、S2m-Sm、S3m-S2m成等差数列Sm,S2m-Sm,S3m-S2m成等比数列(q≠-1 或 m 为奇数)若项的下标成等差数列,则相应的项成等差数列若项的下标成等差数列,则相应的项成等比数列若{an},{bn}成等差数列,则{an+bn},{an-bn}成等差数列{an},{bn}成等比数列,则,,{an·bn}成等比数列一、取倒数法和取对数法求通项例 1 已知数列{an}满足 an+1=,a1=2.求 an.解 对 an+1=两边取倒数得:=,∴=+n+1.令 bn=,则 bn+1=bn+n+1.∴bn=b1+(b2-b1)+(b3-b2)+…+(bn-bn-1)=1+2+3+…+n=1-n.∴an===.例 2 在数列{an}中,an+1=3a,a1=3.求 an.解 由已知,an>0,对 an+1=3a 两边取常用对数得:lg an+1=2lg an+lg 3.令 bn=lg an.则 bn+1=2bn+lg 3.∴bn+1+lg 3=2(bn+lg 3).∴{bn+lg 3}是等比数列,首项是 b1+lg 3=lg 3+lg 3=2lg 3.∴bn+lg 3=2n-1·(b1+lg 3)=2nlg 3.∴bn=(2n-1)lg 3=lg 32n-1=lg an.∴an=32n-1.二、运用恒等变形求数列前 n 项和例 3 已知数列{an}的各项均为正数,Sn为其前 n 项和,对于任意的 n∈N*满足 2Sn=3an-3.(1)求数列{an}的通项公式;(2)设数列{bn}的通项公式是 bn=,前 n 项和为 Tn,求证:对于任意的正数 n,总有 Tn<1.(1)解 由已知得 (n≥2).故 2(Sn-Sn-1)=2an=3an-3an-1,即 an=3an-1 (n≥2).故数列{an}为等比数列,且 q=3.又当 n=1 时,2a1=3a1-3,∴a1=3.∴an=3n.(2)证明 bn==-.∴Tn=b1+b2+…+b...