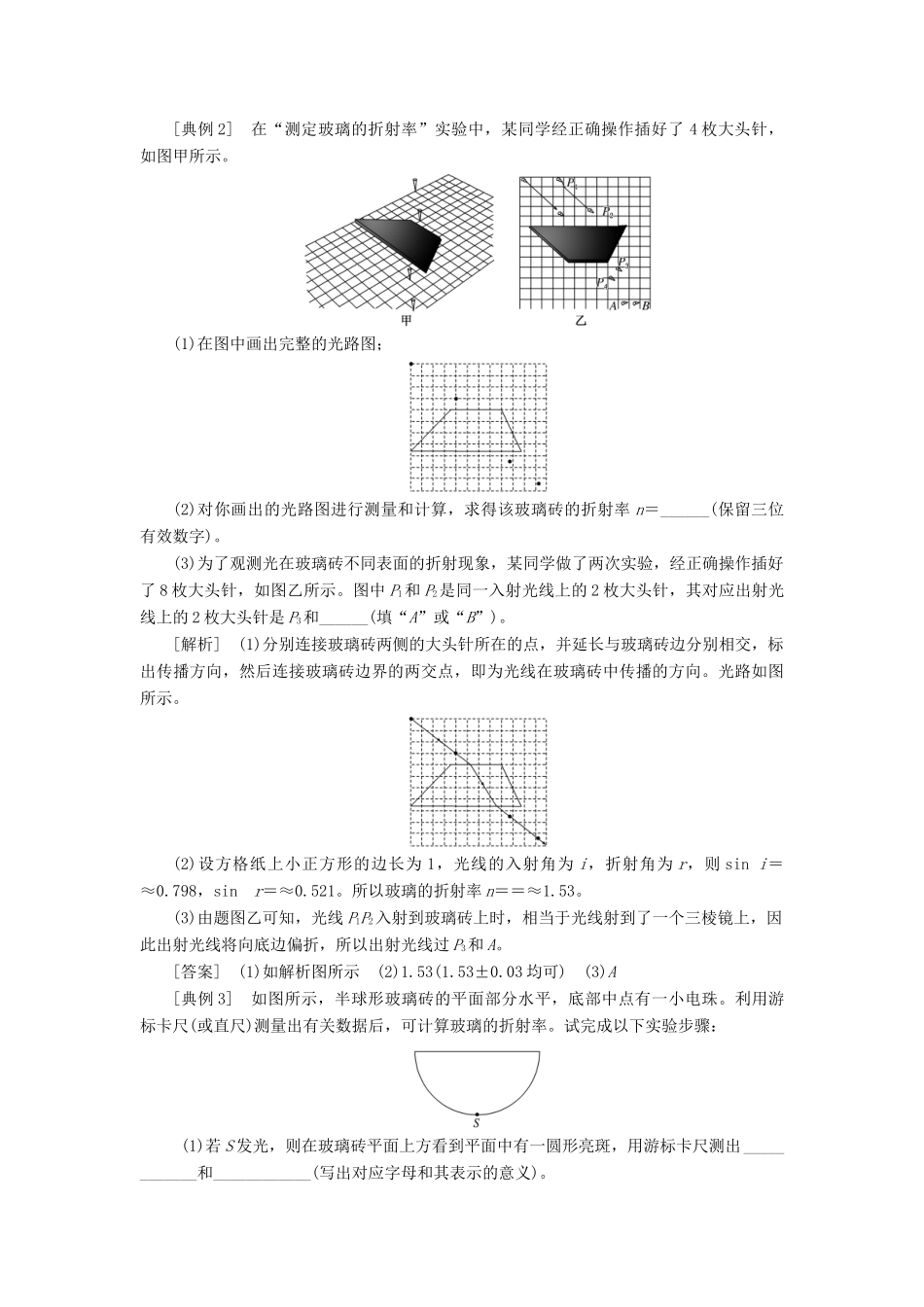
第十三章 光光的折射、全反射现象的分析计算1.几何光学是以光线为工具研究光的传播规律的,所以解决几何光学问题的关键是根据“光的传播规律”画出光路图,然后再利用几何学知识,寻找相应的边角关系。(1)几何光学主要包括四条原理:①光的直线传播规律;②光的反射定律;③光的折射定律;④光路可逆原理。(2)解题时常用的三个公式:① 折射定律公式:n12=;②折射率与光速的关系 n=;③全反射的临界角 sin C=。(3)注意法线的画法:法线画成虚线;法线垂直于界面,如果界面是圆面,则法线垂直于圆的切线,即法线沿半径指向圆心。2.测折射率的方法测折射率常见的方法有成像法、插针法及全反射法,不同方法的实质都相同,由折射定律 n=知,只要确定出入射角 θ1及折射角 θ2即可测出介质的折射率。[典例 1] 如图所示,在一个很大的透明容器中有折射率 n=的透明液体,液体内有一平面镜 M,水平光束 AB 射到容器的竖直侧壁上的 B点后投射到平面镜上 O 点处。为了使光束 BO 经 M 一次反射后的光线能够射出液体的上表面,平面镜与水平方向的夹角 α 应满足什么条件?[解析] 当光经平面镜反射后,经折射从水中射出。但由于平面镜与水平方向的夹角α 的不同取值,光既可向左上方,也可向右上方射出,并可能出现光的全反射。图甲和图乙为反射光恰好能够射出液体上表面的两个光路图。若在水面上发生全反射,有 n=,即 sin C==,C=45°。由几何关系得:图甲中,2(90°-α)+C=90°,即 α=67.5°;图乙中,C+2α=90°,即 α=22.5°。综合两种情况得出:使光束经 M 一次反射后的光线能够射出液体的上表面,平面镜与水平方向的夹角 α 的范围为 22.5°<α<67.5°。[答案] 22.5°<α<67.5°[典例 2] 在“测定玻璃的折射率”实验中,某同学经正确操作插好了 4 枚大头针,如图甲所示。(1)在图中画出完整的光路图;(2)对你画出的光路图进行测量和计算,求得该玻璃砖的折射率 n=______(保留三位有效数字)。(3)为了观测光在玻璃砖不同表面的折射现象,某同学做了两次实验,经正确操作插好了 8 枚大头针,如图乙所示。图中 P1和 P2是同一入射光线上的 2 枚大头针,其对应出射光线上的 2 枚大头针是 P3和______(填“A”或“B”)。[解析] (1)分别连接玻璃砖两侧的大头针所在的点,并延长与玻璃砖边分别相交,标出传播方向,然后连接玻璃砖边界的两交点,即为光线在玻璃砖中传播的方向。光路如...