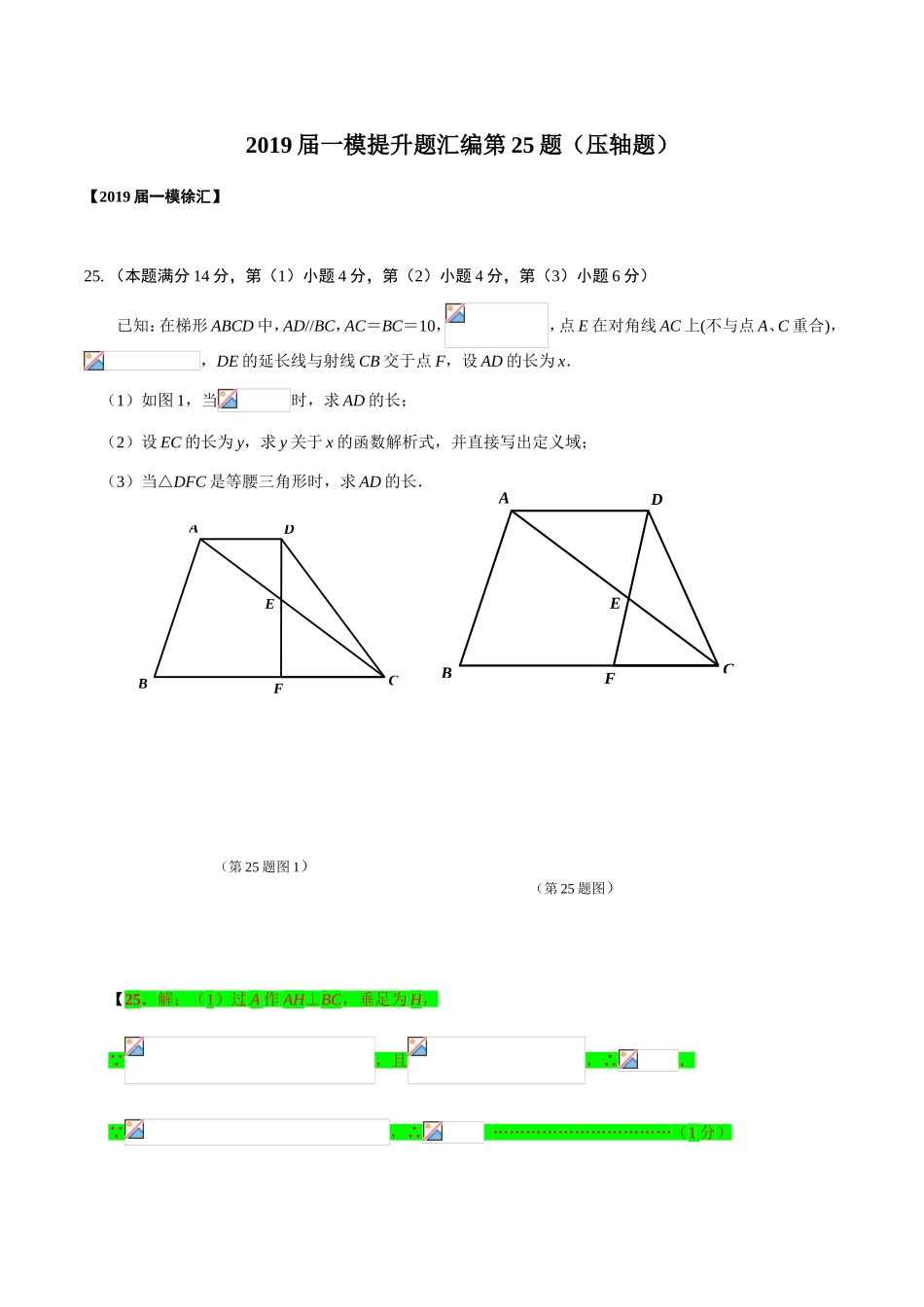
FEACBDFEACBD2019届一模提升题汇编第25题(压轴题)【2019届一模徐汇】25.(本题满分14分,第(1)小题4分,第(2)小题4分,第(3)小题6分)已知:在梯形ABCD中,AD//BC,AC=BC=10,,点E在对角线AC上(不与点A、C重合),,DE的延长线与射线CB交于点F,设AD的长为x.(1)如图1,当时,求AD的长;(2)设EC的长为y,求y关于x的函数解析式,并直接写出定义域;(3)当△DFC是等腰三角形时,求AD的长.【25.解:(1)过A作AH⊥BC,垂足为H, ,且,∴. ,∴……………………………(1分)(第25题图1)(第25题图)∴, ∥,∴,∴四边形AHFD是矩形,∴ …………………………(1分)∴……………………………………………(1分)∴……………………………………………………………(1分)(2) ∥,∴. ,∴. ,∴∽………………………………………(1分)∴, ,∴…………………………………(1分) ∴且……………(2分)(3)由,得:∽,又∥有∽,∴∽∴当是等腰三角形时,也是等腰三角形………………………(1分)∴………………………………………………………(1分)……………………………………………………………(2分)………………………………………(2分)∴综上所述,当是等腰三角形时,AD的长是.】【2019届一模浦东】25.(本题满分14分,其中第(1)小题3分,第(2)小题5分,第(3)小题6分)将大小两把含30°角的直角三角尺按如图10-1位置摆放,即大小直角三角尺的直角顶点C重合,小三角尺的顶点D、E分别在大三角尺的直角边AC、BC上,此时小三角尺的斜边DE恰好经过大三角尺的重心G.已知∠A=∠CDE=30°,AB=12.(1)求小三角尺的直角边CD的长;(2)将小三角尺绕点C逆时针旋转,当点D第一次落在大三角尺的边AB上时(如图10-2),求点B、E之间的距离;(3)在小三角尺绕点C旋转的过程中,当直线DE经过点A时,求∠BAE的正弦值.G(图10-1)(图10-2)EDCABDCBAE【25、(1);(2);(3)或】【2019届一模杨浦】25.(本题满分14分,第(1)小题4分,第(2)、(3)小题各5分)已知:梯形ABCD中,AD//BC,AB⊥BC,AD=3,AB=6,DF⊥DC分别交射线AB、射线CB于点E、F.(1)当点E为边AB的中点时(如图1),求BC的长;(2)当点E在边AB上时(如图2),联结CE,试问:∠DCE的大小是否确定?若确定,请求出∠DCE的正切值;若不确定,则设AE=x,∠DCE的正切值为y,请求出y关于x的函数解析式,并写出定义域;(3)当△AEF的面积为3时,求△DCE的面积.【25.(本题满分14分,第(1)小题4分,第(2)、(3)小题各5分)解:(1) AD//BC,∴. E为AB中点,∴AE=BE.∴AD=BF,DE=EF. AD=3,AB=6,∴BF=3,BE=3.∴BF=BE. AB⊥BC,∴∠F=45°且EF=.(1分)∴DF=2EF=.(1分) DF⊥DC,∠F=45°,∴CF=12.(1分)ABCDEF(图1)(第25题图)ABCDEF(图2)∴BC=.(1分)(2)∠DCE的大小确定,.(1分)作CH⊥AD交AD的延长线于点H,∴∠HCD+∠HDC=90°. DF⊥DC,∴∠ADE+∠HDC=90°.∴∠HCD=∠ADE.又 AB⊥AD,∴∠A=∠CHD.∴△AED∽△HDC.(2分)∴.(1分) AB⊥AD,CH⊥AD,AD//BC,∴CH=AB=6. AD=3,CH=6,∴.即.(1分)(3)当点E在边AB上,设AE=x, AD//BC,∴,即.∴. △AEF的面积为3,∴.∴.(1分) AD=3,AB⊥AD,∴DE=5. ,∴DC=10. DF⊥DC,∴.(1分)当点E在边AB延长线上,设AE=y, AD//BC,∴,即.∴. △AEF的面积为3,∴.∴.(1分) AD=3,AB⊥AD,∴DE=.ABCDEF联结CE,作CH⊥AD交AD的延长线于点H,同(1)可得.(1分)∴DC= DF⊥DC,∴.(1分)综上,当△AEF的面积为3时,△DCE的面积为25或73.】【2019届一模普陀】25.(本题满分14分)如图11,点在线段AB上,,,点C是射线OP上的一个动点.(1)如图11①,当,,求的值;(2)如图11②,当AC=AB时,求的长(用含的代数式表示);(3)在第(2)题的条件下,过点A作AQ∥BC,并使∠QOC=∠B,求的值.ABCPOABCPO图11①图11②【25.解:(1)过点作,为垂足.(1分)∴.在Rt△中,,.∴,.(1分) ,∴,. ,∴. ,∴.∴. ,∴△∽△.(1分)∴.∴.∴.(1分)∴,(不合题意,舍去...