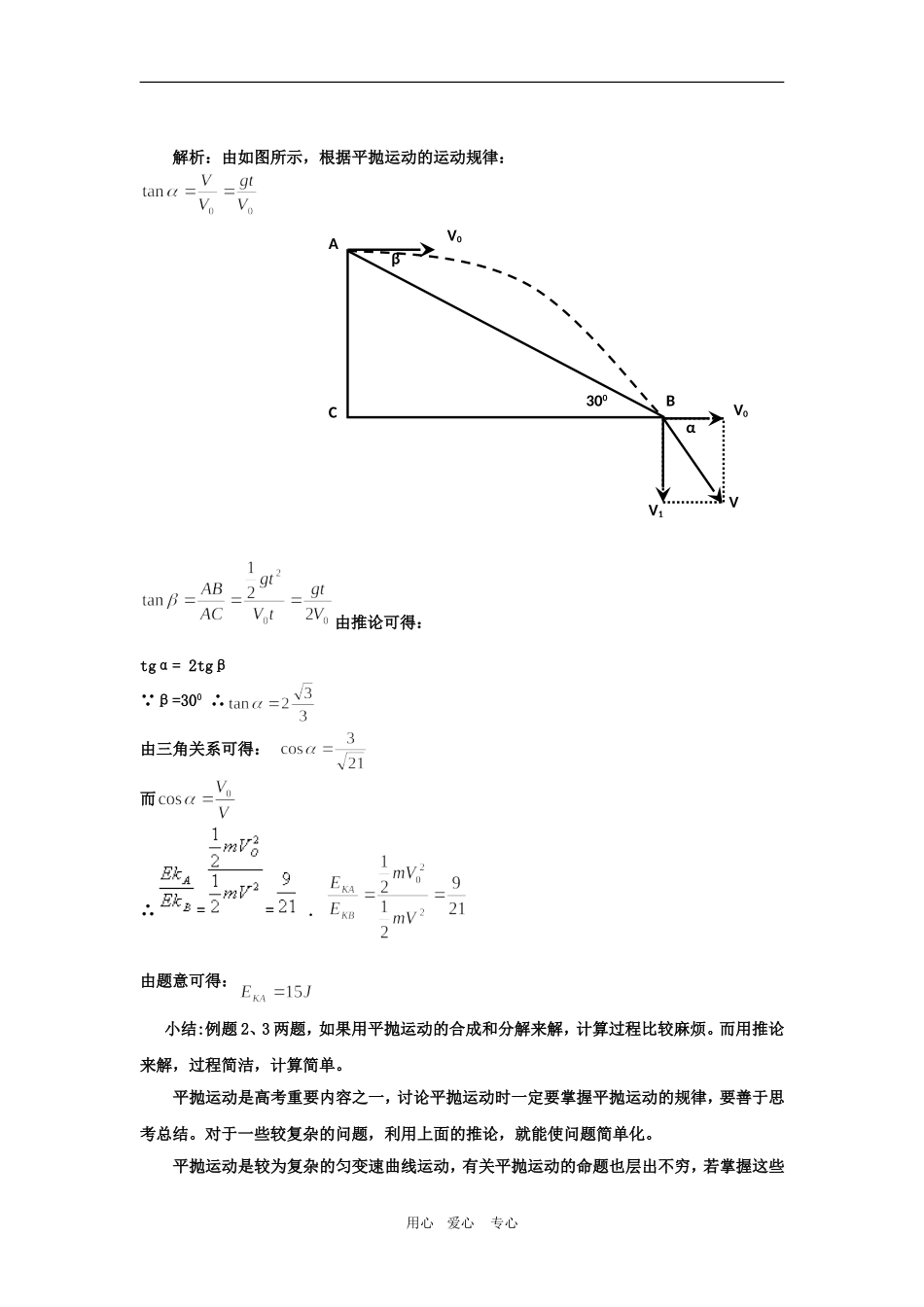
平抛运动的一个重要的推论及其妙用平抛运动是匀变速曲线运动中的常见运动,它可以看作由匀速直线运动和自由落体合成。因此也是两个直线运动合成后为曲线运动的典型实例,其基本规律和处理方法一直是各类考试的热点。下面介绍平抛运动中的一个重要结论及其妙用,供大家参考。一、平抛运动的特点1.平抛运动可以分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动两个分运动的合成。在水平方向上的速度 vx=v0,位移 x=v0t。在竖直方向上的速度 vy=gt,位移y=gt2。所以平抛运动的合速度 vt=,合位移 s=,速度与水平方向上的夹角=arctan,位移与水平方向上的夹角=arctan,两个夹角的关系 tan=2tan。其规律可以表示为如下表所示。速度加速度位移图示水平方向vx=v0ax=0x=v0t竖直方向vy=gtay=gy=gt2平抛运动vt=tan=a=g竖直向下s=tan=2.平抛运动除常规的按照水平和竖直方向来分解以外,还可以根据需要向其它的方向分解出其它的不同的运动。由平抛运动的处理思路,也使我们明确了其它匀变速曲线运动的处理方法,即把力或者速度正交分解力和垂直与力的方向上(或速度和垂直与速度方向上)的不同的运动3.有一些运动从初速度和受力情况上看和平抛运动类似——类平抛运动,也可以用平抛运动的处理思路来解决。二、平抛运动的一个重要推论平抛运动的速度方向和位移方向不在一条直线上,如图所示,位移 s 与水平方向的夹角 小于速度与水平方向的夹角。由几何关系:tan ==x=v0ty=gt2=vyt用心 爱心 专心项目内容svvxvyxyOAxAyAsvvxvyxyOAxAyA联立三式,解得 tan ==2tan这个关系说明速度方向与水平方向的夹角与位移方向与水平方向的夹角之间的关系。同样的这一结论也适用于类平抛运动。推论:做平抛运动的物体经过一段时间,到达某一位置时,设其末速度与水平方向的夹角为α,位移与水平方向的夹角为 β,则 tgα=2tgβ。三、推论的妙用 例题 1:作平抛运动的物体,当它的水平速度与竖直速度的要大小之比为 1:2 时,其水平位移与竖直位移的大小之比_________。 解析:设平抛运动物体的初速度为 V0,从 O点水平抛出,经过一段时间,到达 A 点。由图所示。根据平抛运动的运动规律可得:由推论可得:tgα= 2tgβ tgα=2∴tgβ=1 即 AC:AB=1:1 . 例题 2:如图,从倾角为 θ 的足够长斜面的 A 点先后将同一个小球以不同的初速度水平向右抛出,第一次初速度...