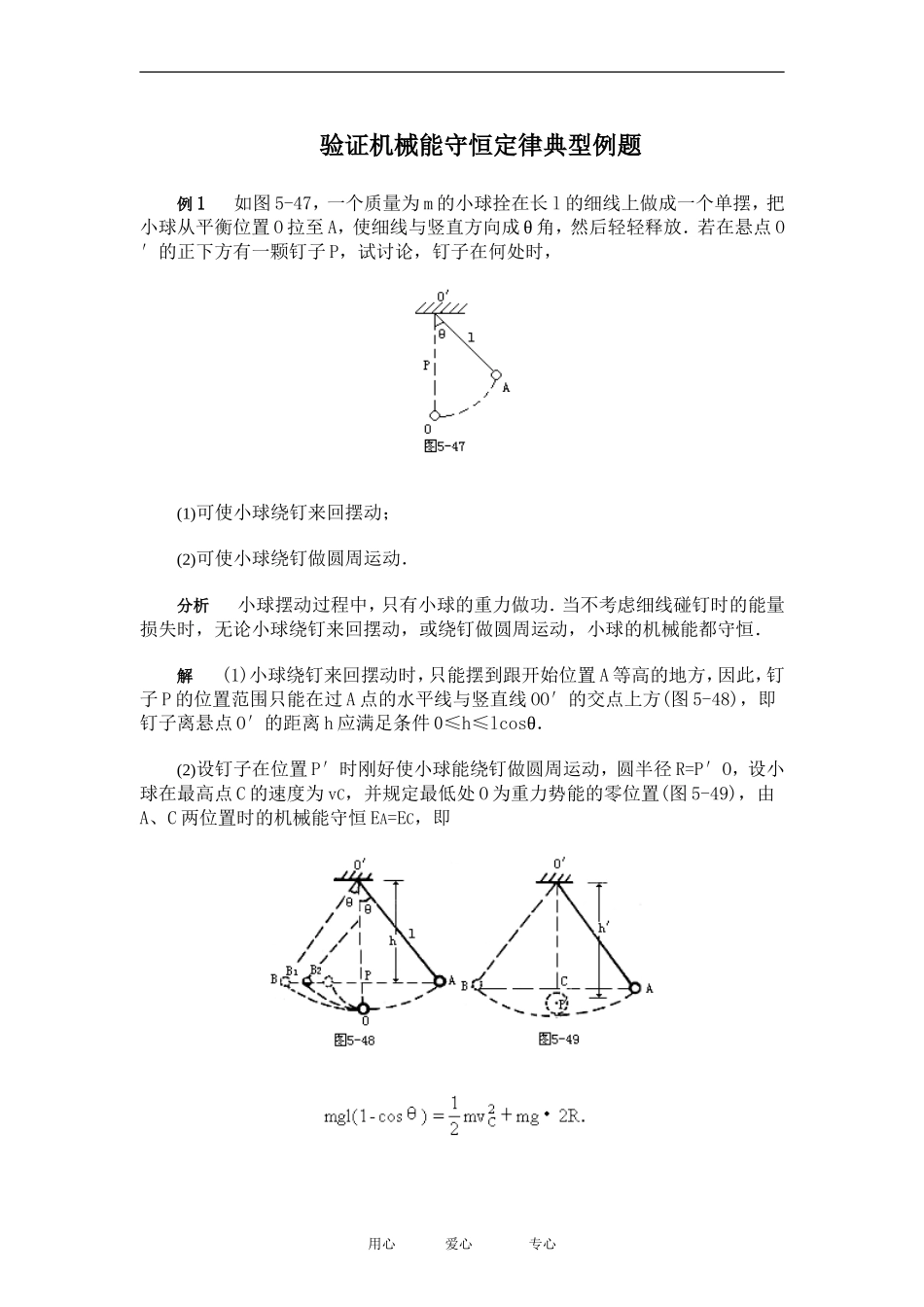
验证机械能守恒定律典型例题例 1 如图 5-47,一个质量为 m 的小球拴在长 l 的细线上做成一个单摆,把小球从平衡位置 O 拉至 A,使细线与竖直方向成 θ 角,然后轻轻释放.若在悬点 O′的正下方有一颗钉子 P,试讨论,钉子在何处时,(1)可使小球绕钉来回摆动;(2)可使小球绕钉做圆周运动.分析 小球摆动过程中,只有小球的重力做功.当不考虑细线碰钉时的能量损失时,无论小球绕钉来回摆动,或绕钉做圆周运动,小球的机械能都守恒.解 (1)小球绕钉来回摆动时,只能摆到跟开始位置 A 等高的地方,因此,钉子 P 的位置范围只能在过 A 点的水平线与竖直线 OO′的交点上方(图 5-48),即钉子离悬点 O′的距离 h 应满足条件 0≤h≤lcosθ.(2)设钉子在位置 P′时刚好使小球能绕钉做圆周运动,圆半径 R=P′O,设小球在最高点 C 的速度为 vC,并规定最低处 O 为重力势能的零位置(图 5-49),由A、C 两位置时的机械能守恒 EA=EC,即用心 爱心 专心 ①又因为刚好能越过 C 点做圆运动,此时绳中的张力为零,由重力提供向心力,即 ②所以钉子 P′离悬点 O′的距离如果钉子位置从 P′处继续下移,则小球将以更大的速度越过圆周的最高点,此时可由绳子的张力补充在最高点时所需的向心力,仍能绕钉子做圆周运动.所以,在绕钉做圆运动时,钉子离悬点的距离 h′应满足条件 说明 由本题的解答可知,位置 P 是小球能绕钉来回摆动的最低位置;位置P′是小球能绕钉做圆周运动的最高位置.如钉子在 PP′之间,则悬线碰钉后,先绕钉做圆运动,然后将在某一位置上转化为斜抛运动.例 2 一内壁光滑的环形细圆管,位于竖直平面内,环的半径为 R(比细管的半径大得多).在圆管中有两个直径与细管内径相同的小球(可视为质点).A 球的质量为 m1,B 球的质量为 m2.它们沿环形圆管顺时针运动,经过最低点时的速度都为 v0 设 A 球运动到最低点时,B 球恰好运动到最高点,若要此时两球作用于圆管的合力为零,那么 m1、m2、R 与 v0 应满足的关系式是____.分析 A 球运动到最低点时,由外壁对它产生的弹力 NA 和 A 球重力 m1g 的合力作为向心力,即用心 爱心 专心 ①A 球对外壁产生的压力 NA′大小等于 NA,方向沿半径背离圆心(图 5-50).要求对圆管的合力为零,B 球在最高点时也必须对外壁(不可能是内壁)产生一个等量的压力 NB′.因此,B 球在最高点有向外壁挤压的作用,由外壁对它产生的弹...