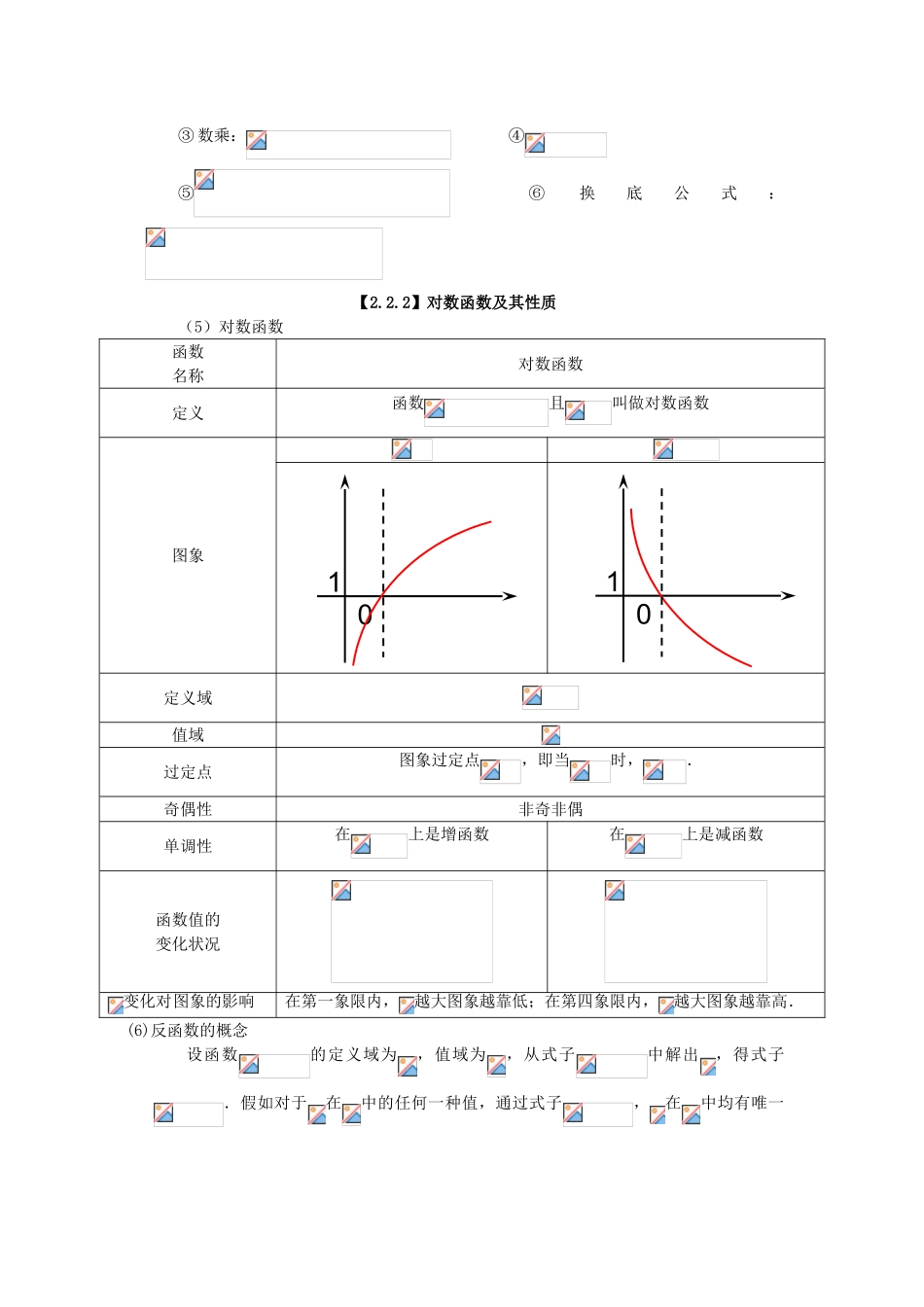
第二章 基本初等函数(Ⅰ)〖2.1〗指数函数【2.1.1】指数与指数幂的运算(1)根式的概念① 假如,且,那么叫做的次方根.当是奇数时,的次方根用符号表达;当是偶数时,正数的正的次方根用符号表达,负的次方根用符号表达;0 的次方根是 0;负数没有次方根.② 式子叫做根式,这里叫做根指数,叫做被开方数.当为奇数时,为任意实数;当为偶数时,.③ 根 式 的 性 质 :; 当为 奇 数 时 ,; 当为 偶 数 时 , .(2)分数指数幂的概念① 正数的正分数指数幂的意义是:且.0 的正分数指数幂等于 0.② 正数的负分数指数幂的意义是:且.0 的负分数指数幂没故意义. 注意口诀:底数取倒数,指数取相反数.(3)分数指数幂的运算性质① ②③【2.1.2】指数函数及其性质(4)指数函数函数名称指数函数定义函数且叫做指数函数图象0101定义域值域过定点图象过定点,即当时,.奇偶性非奇非偶单调性在上是增函数在上是减函数函数值的变化状况变化对图象的影响在第一象限内,越大图象越高;在第二象限内,越大图象越低.〖2.2〗对数函数【2.2.1】对数与对数运算(1)对数的定义 ① 若,则叫做以为底的对数,记作,其中叫做底数,叫做真数.② 负数和零没有对数.③ 对数式与指数式的互化:.(2)几种重要的对数恒等式,,.(3)常用对数与自然对数常用对数:,即;自然对数:,即(其中…).(4)对数的运算性质 假如,那么① 加法: ②减法:③ 数乘: ④⑤ ⑥换底公式:【2.2.2】对数函数及其性质(5)对数函数函数名称对数函数定义函数且叫做对数函数图象定义域值域过定点图象过定点,即当时,.奇偶性非奇非偶单调性在上是增函数在上是减函数函数值的变化状况变化对图象的影响在第一象限内,越大图象越靠低;在第四象限内,越大图象越靠高.(6)反函数的概念设函数的定义域为,值域为,从式子中解出,得式子.假如对于在中的任何一种值,通过式子,在中均有唯一0101确定的值和它对应,那么式子表达是的函数,函数叫做函数的反函数,记作,习惯上改写成.(7)反函数的求法① 确定反函数的定义域,即原函数的值域;②从原函数式中反解出;③ 将改写成,并注明反函数的定义域.(8)反函数的性质 ① 原函数与反函数的图象有关直线对称.② 函数的定义域、值域分别是其反函数的值域、定义域.③ 若在原函数的图象上,则在反函数的图象上.④ 一般地,函数要有反函数则它必须为单调函数.〖2.3〗幂函数(1...