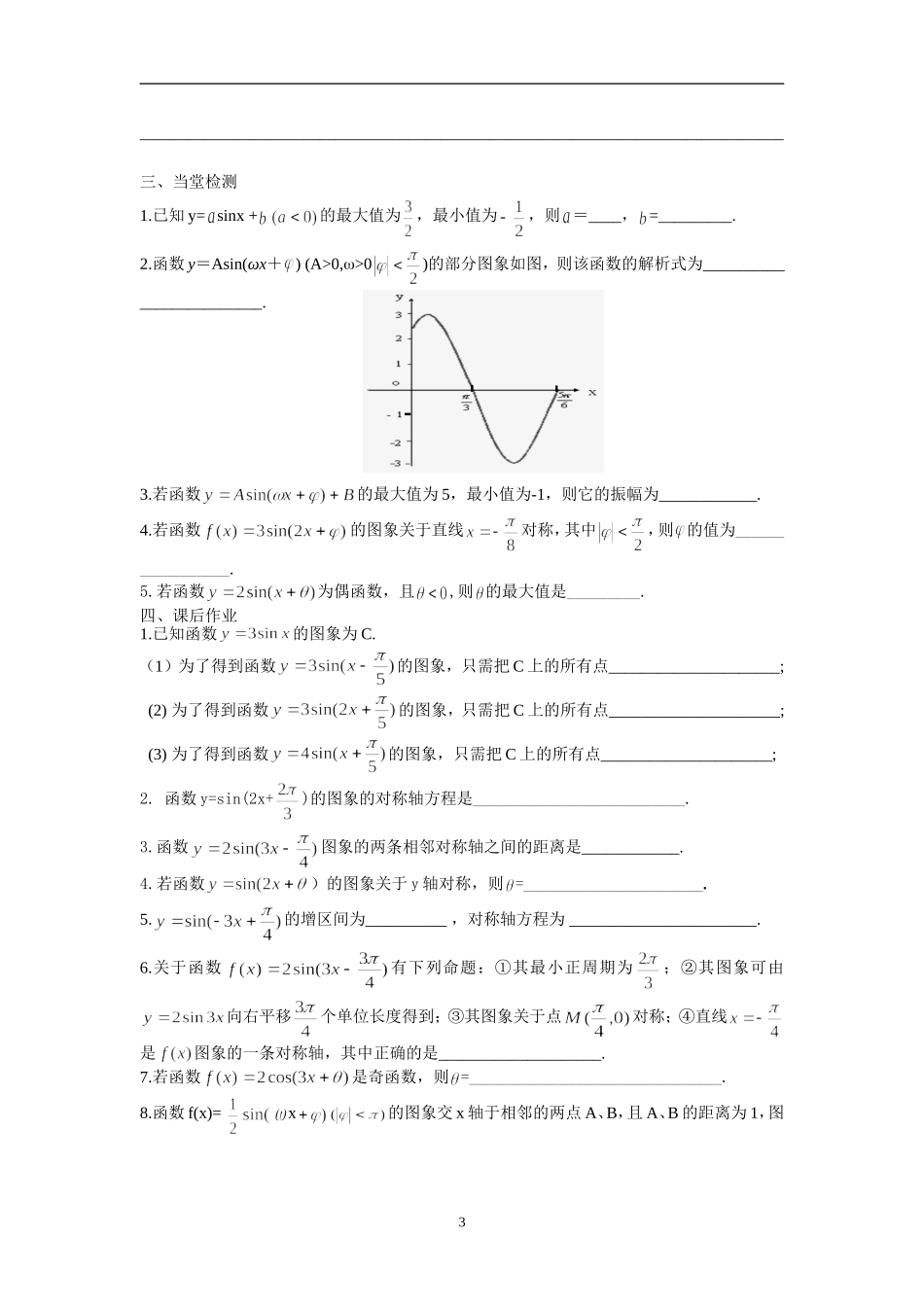
1.3.3 函数的图象(2)【学习目标】1.理解由 y=sinx 的图象逐步向变换的过程,会用三角函数的图象和性质解决一些简单的问题;2.会由图象求函数的解析式,解决有关简单的问题;3.进一步体会数形结合的魅力,体会化归的思想方法.【学习重点、难点】函数的图象和性质【学习过程】一、复习1.函数的振幅、周期、初相各是多少?它的图象可由函数 y=sinx 的图象经过怎样的变换而得到?2.求函数图象的对称轴和对称中心.二、典型例题例 1、已知函数,(1)求函数的最小正周期;(2)用五点法作出函数的图象,并说明该函数的图象可以由的图象怎样变换得到?(3)求函数的最大值及取得最大值时 的集合;(4)求函数的单调递增区间;1例 2、如下图是函数 f(x)=Asin(ωx+ )(其中 A>0,| |<)的图象的一部分,求 f(x)的解析式. 练习、已知点 M(,3)是函数(A>0,)的图象的一个最高点,且点 N()是图象上与点 M 相邻的一个最低点,求此函数的解析式.小结:由函数的图象(或图象特征)求函数的表达式的一般步骤是:例 3、弹簧挂着的小球上、下振动,它在时间时离开平衡位置(就是静止时的位置)的距离由函数关系式决定:.(1)以 为横坐标, 为纵坐标作出函数的图象();(2)求小球开始振动的位置;(3)经过多长时间,小球往返振动一次?(4)每秒钟内小球能往返振动多少次?回顾反思: _______________________________________________________________________________2_______________________________________________________________________________三、当堂检测1.已知 y= sinx +的最大值为,最小值为,则 =____, =_________.2.函数 y=Asin(ωx+ ) (A>0,w>0)的部分图象如图,则该函数的解析式为_________________________.3.若函数的最大值为 5,最小值为-1,则它的振幅为____________.4.若函数的图象关于直线对称,其中,则 的值为_________________.5.若函数为偶函数,且,则 的最大值是_________.四、课后作业 1.已知函数的图象为 C.(1)为了得到函数的图象,只需把 C 上的所有点_____________________;(2) 为了得到函数的图象,只需把 C 上的所有点_____________________;(3) 为了得到函数的图象,只需把 C 上的所有点_____________________;2. 函数 y=sin(2x+)的图象的对称轴方程是__________________________.3.函数图象的两条相邻对称轴之间的距离是____________.4.若函数)的图象关于 y...