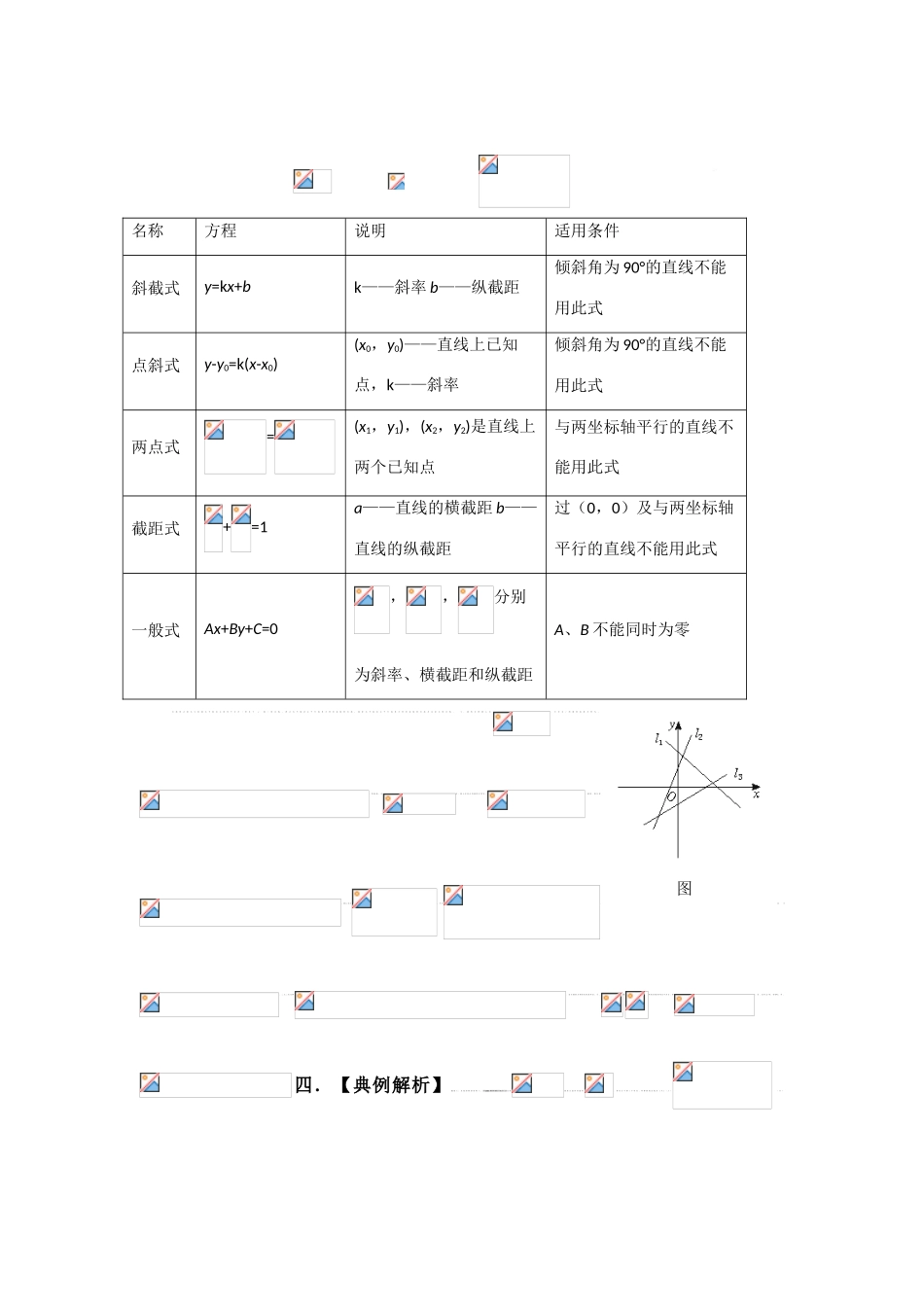
2010 年高考数学一轮复习精品学案(人教版 A 版)直线与圆的方程一.【课标要求】1.直线与方程(1)在平面直角坐标系中,结合具体图形,探索确定直线位置的几何要素;(2)理解直线的倾斜角和斜率的概念,经历用代数方法刻画直线斜率的过程,掌握过两点的直线斜率的计算公式;(3)根据确定直线位置的几何要素,探索并掌握直线方程的几种形式(点斜式、两点式及一般式),体会斜截式与一次函数的关系;2.圆与方程回顾确定圆的几何要素,在平面直角坐标系中,探索并掌握圆的标准方程与一般方程。二.【命题走向】直线方程考察的重点是直线方程的特征值(主要是直线的斜率、截距)有关问题,可与三角知识联系;圆的方程,从轨迹角度讲,可以成为解答题,尤其是参数问题,在对参数的讨论中确定圆的方程。预测 2010 年对本讲的考察是:(1)2 道选择或填空,解答题多与其他知识联合考察,本讲对于数形结合思想的考察也会是一个出题方向;(2)热点问题是直线的倾斜角和斜率、直线的几种方程形式和求圆的方程.三.【要点精讲】1.倾斜角:一条直线 L 向上的方向与 X 轴的正方向所成的最小正角,叫做直线的倾斜角,范围为。2.斜率:当直线的倾斜角不是 900时,则称其正切值为该直线的斜率,即 k=tan;当直线的倾斜角等于 900时,直线的斜率不存在.过两点 p1(x1,y1),p2(x2,y2)(x1≠x2)的直线的斜率公式:k=tan(若 x1=x2,则直线 p1p2的斜率不存在,此时直线的倾斜角为 900)。4.直线方程的五种形式确定直线方程需要有两个互相独立的条件。确定直线方程的形式很多,但必须注意各种形式的直线方程的适用范围。名称方程说明适用条件斜截式y=kx+bk——斜率 b——纵截距倾斜角为 90°的直线不能用此式点斜式y-y0=k(x-x0)(x0,y0)——直线上已知点,k——斜率倾斜角为 90°的直线不能用此式两点式=(x1,y1),(x2,y2)是直线上两个已知点与两坐标轴平行的直线不能用此式截距式+=1a——直线的横截距 b——直线的纵截距过(0,0)及与两坐标轴平行的直线不能用此式一般式Ax+By+C=0,,分别为斜率、横截距和纵截距A、B 不能同时为零直线的点斜式与斜截式不能表示斜率不存在(垂直于x 轴)的直线;两点式不能表示平行或重合两坐标轴的直线;截距式不能表示平行或重合两坐标轴的直线及过原点的直线。5.圆的方程圆心为,半径为r的圆的标准方程为:。 特 殊 地 , 当时 , 圆 心 在 原 点 的 圆 的 方 程 为 :。 圆 的...