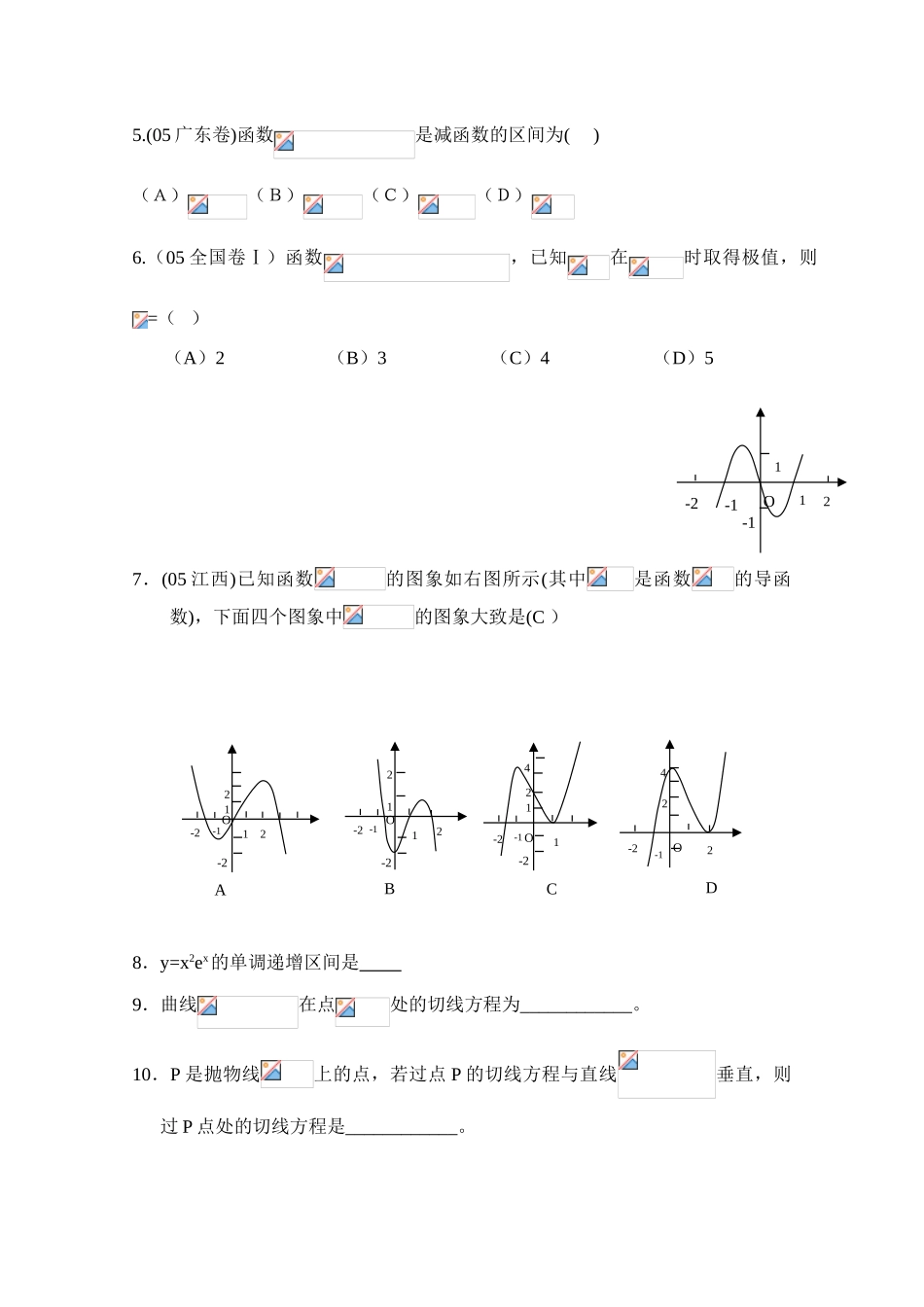
导数的综合应用(1)一、问题的提出:利用导数直接可以解决许多问题,例如,求曲线的切线,函数的单调区间,函数的极值等. 同时导数也常与其它知识交汇考查,如不等式、三角、数列、解析几何等等.我们以近年高考试题为主,讨论导数的综合应用问题二、例题分析 例 1.(04 年重庆卷.理 20)设函数. (Ⅰ)求导数,并证明有两个不同的极值点; (Ⅱ)若不等式成立,求的取值范围.例 2.(04 年全国卷二.理 22)已知函数,.(Ⅰ)求函数的最大值;(Ⅱ)设,证明.例 3.(04 年广东卷.21)设函数,其中常数为整数.(Ⅰ)当为何值时,;(Ⅱ)定理:若函数在上连续,且与异号,则至少存在一点,使得.试用上述定理证明:当整数时,方程在内有两个实根例 4.(05 全国卷Ⅱ)设 a 为实数,函数 (Ⅰ)求的极值. (Ⅱ)当 a 在什么范围内取值时,曲线轴仅有一个交点.例 5.(05 辽宁卷) 函数在区间(0,+∞)内可导,导函数是减函数,且 设是曲线在点()得的切线方程,并设函数 (Ⅰ)用、、表示 m; (Ⅱ)证明:当; (Ⅲ)若关于的不等式上恒成立,其中 a、b 为实数, 求 b 的取值范围及 a 与 b 所满足的关系.四、作业 导数的综合应用(1)1.曲线 y=x3在 P 点处的切线斜率为 k,若 k=3,则 P 点为( )(A)(-2,-8) (B)(-1,-1)或(1,1) (C)(2,8) (D)(-,-)2.一质点在运动中经过的路程 S 和经历的时间 t 有关系 S=5-3t2,则它在[1,+△t]内的平均速度为( )(A)3△t+6 (B)-3△t+6 (C)3△t-6 (D)-3△t-63.曲线 y=x3-x2+5,过其上横坐标为 1 的点作曲线的切线,则切线的倾斜角为( )(A) (B) (C) (D)4.过曲线 y=x2上一点作切线与直线 3x-y+1=0 交成 450角,则切点坐标为( )(A)(-1,1) (B) (,)或(1,1)(C)(,)或(-1,1) (D)(-1,1)或(1,1)-22O1-1-115.(05 广东卷)函数是减函数的区间为( )(A)(B)(C)(D)6.(05 全国卷Ⅰ)函数,已知在时取得极值,则=( )(A)2(B)3(C)4(D)57.(05 江西)已知函数的图象如右图所示(其中是函数的导函数),下面四个图象中的图象大致是(C )8.y=x2ex的单调递增区间是 9.曲线在点处的切线方程为____________。10.P 是抛物线上的点,若过点 P 的切线方程与直线垂直,则过 P 点处的切线方程是____________。 O-221-1-212O-2-221-112O-241-1-212O-22...