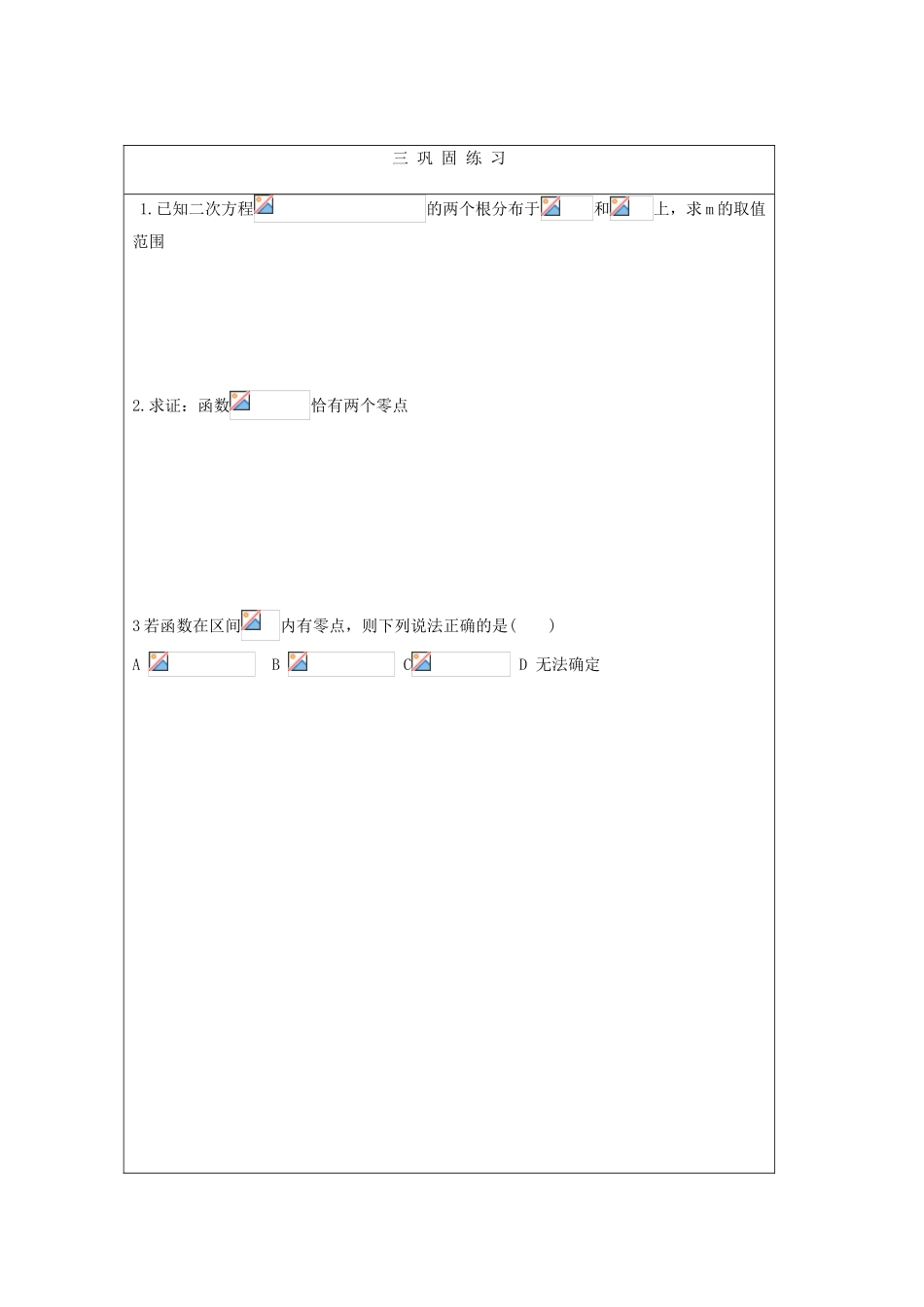
教案、学案用纸第四章利用函数性质判定方程解的存在年级高一学科数学课题第四章利用函数性质判定方程解的存在授课时间撰写人学习重点了解函数与方程之间的内在联系学习难点掌握函数零点的判定定理,会判定方程解的个数学 习 目 标1.理解函数的零点与方程根的关系.2.会判断一元二次方程根的存在性及根的个数.3 会判定方程在给定区间上解的个数.教 学 过 程一 自 主 学 习1. 求下列函数的零点.(1)f(x)=-x2-2x+3 (2)f(x)=x4-12. 判断方程解的存在.(1)2x2-3x+1=0 (2)lnx-x+2=0二 师 生 互动例1.方程 lnx+2x-6=0 的根一定位于区间( )A.(1,2) B.(2,3) C.(3,4) D.(4,5)例 2 (1)若方程在(0,1)内恰有一解,则实数 a 的取值范围. (2)已知函数,若在上存在使,则实数 m 的取值范围三 巩 固 练 习1.已知二次方程的两个根分布于和上,求 m 的取值范围2.求证:函数恰有两个零点3 若函数在区间内有零点,则下列说法正确的是( )A B C D 无法确定四 课 后 反 思五 课 后 巩 固 练 习1. 设函数,若,则方程的解的个数是 ( )A 1 B 2 C 3 D 43. 判断方程有两相异的实数解,且有一个大于 5,一个小于。3.若关于的方程在(0,1)内恰有一个解,求实数 a 的取值范围