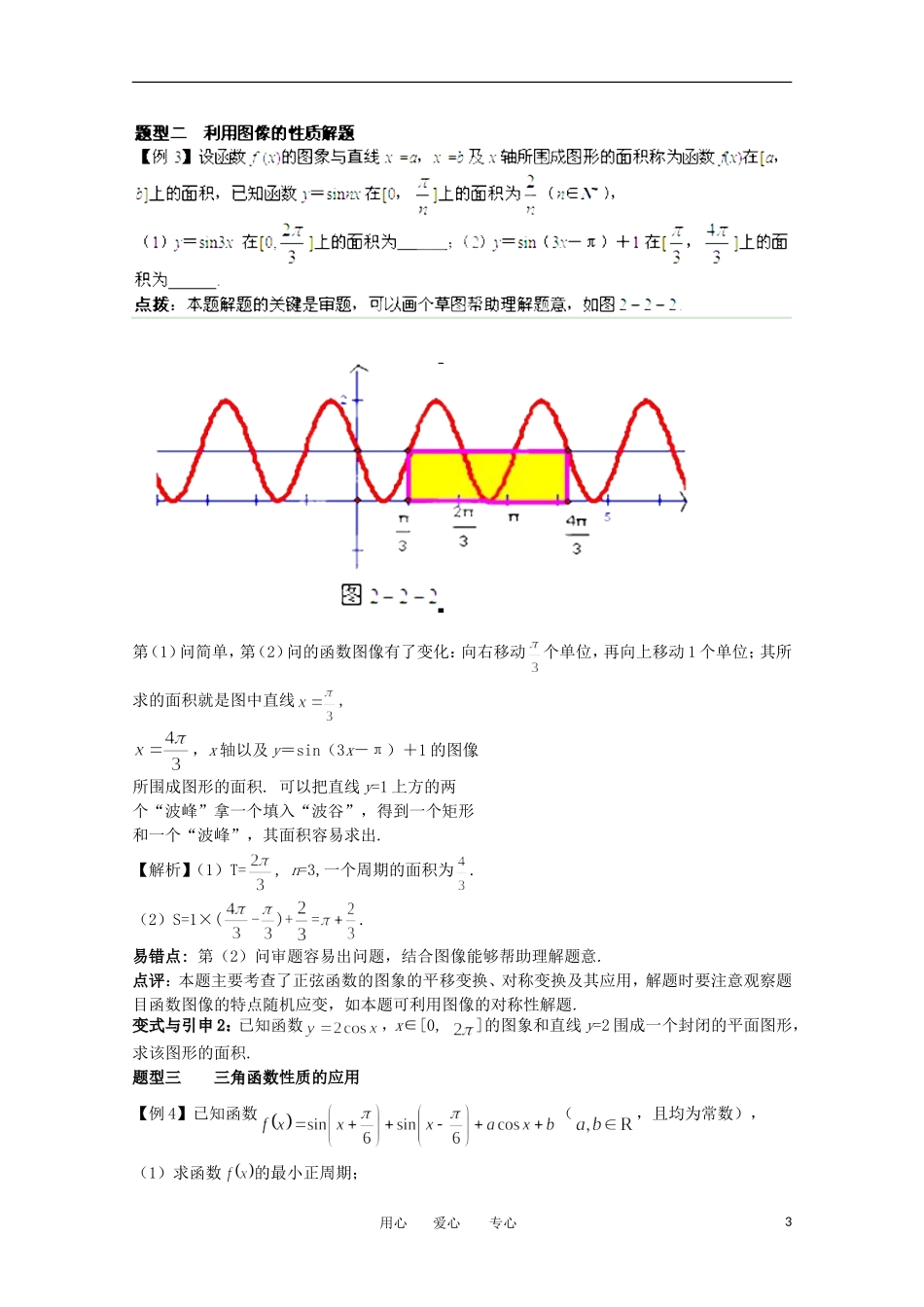
第二节 三角函数的图像、性质及其变换近几年高考对“三角函数”一章三角的考查要求略有降低,而对三角函数的图像、性质的考查有逐步加强的趋势. “考试大纲”将三角函数的图象和性质,由“了解”改为“理解”,提高了一个层次.因此,考生在复习中要作出相应的调整.它们的难度值一般控制在 0.5-0.8 之间,且在解答题中大多需要利用三角函数的变换和性质求解. 考试要求 ⑴理解正弦函数、余弦函数的定义、性质,理解正切函数的单调性;⑵了解函数的 物 理 意 义 , 会 用 “ 五 点 法 ” 画 正 弦 函 数 、 余 弦 函 数 和 函 数y=Asin(ωx+φ)的简图,了解参数 对函数图像变化的影响.题型一 题型一 由“参”定“形”,由“形”定“参”【例 1】 点拨:(1)在函数 y=Asin(ωx+j)的有关问题中,只要确定了这三个参数 A,ω,φ,则该函数的图像、性质等就出来了;同理,(2)中,已知图像求解析式问题,关键也是确定三个参数A,ω,φ,最困难的就是求 φ.用心 爱心 专心1于是,本题的答案为②、③.例 2.已知函数的图象如图所示,则它的解析式为.点拨:已知图像求解析式问题,关键也是确定三个参数 A,ω,φ,尤其是求 φ.解析:由图知 以下求 j 的值有多种方法可供选择:易错点 例(1)中,选项“”的含义容易被误解;例(2)中,已知图像求解析式中的 φ 时,常常由于方法不当或范围不清晰而不能求出准确值.点评:三角函数的图像由若干个参数确定(即由“参”定“形”),同时,已知三角函数的图像也能够确定这若干个参数(即由“形”定“参”).本例所用的方法带有普遍性,用来求解有关函数 y=Asin(ωx+j)的图象问题十分奏效.变式与引申变式与引申 11::若将函数的图像向右平移个单位长度后,与函数的图像重合,则的最小值为( )A. B. C. D. 用心 爱心 专心2图第(1)问简单,第(2)问的函数图像有了变化:向右移动个单位,再向上移动 1 个单位;其所求的面积就是图中直线,,x 轴以及 y=sin(3x-π)+1 的图像所围成图形的面积. 可以把直线 y=1 上方的两个“波峰”拿一个填入“波谷”,得到一个矩形和一个“波峰”,其面积容易求出.【解析】(1)T=, n=3,一个周期的面积为.(2)S=1×(-)+=.易错点: 第(2)问审题容易出问题,结合图像能够帮助理解题意.点评:本题主要考查了正弦函数的图象的平移变换、对称变换及其应用,解题时要注意观察题目函数图像的特点随...