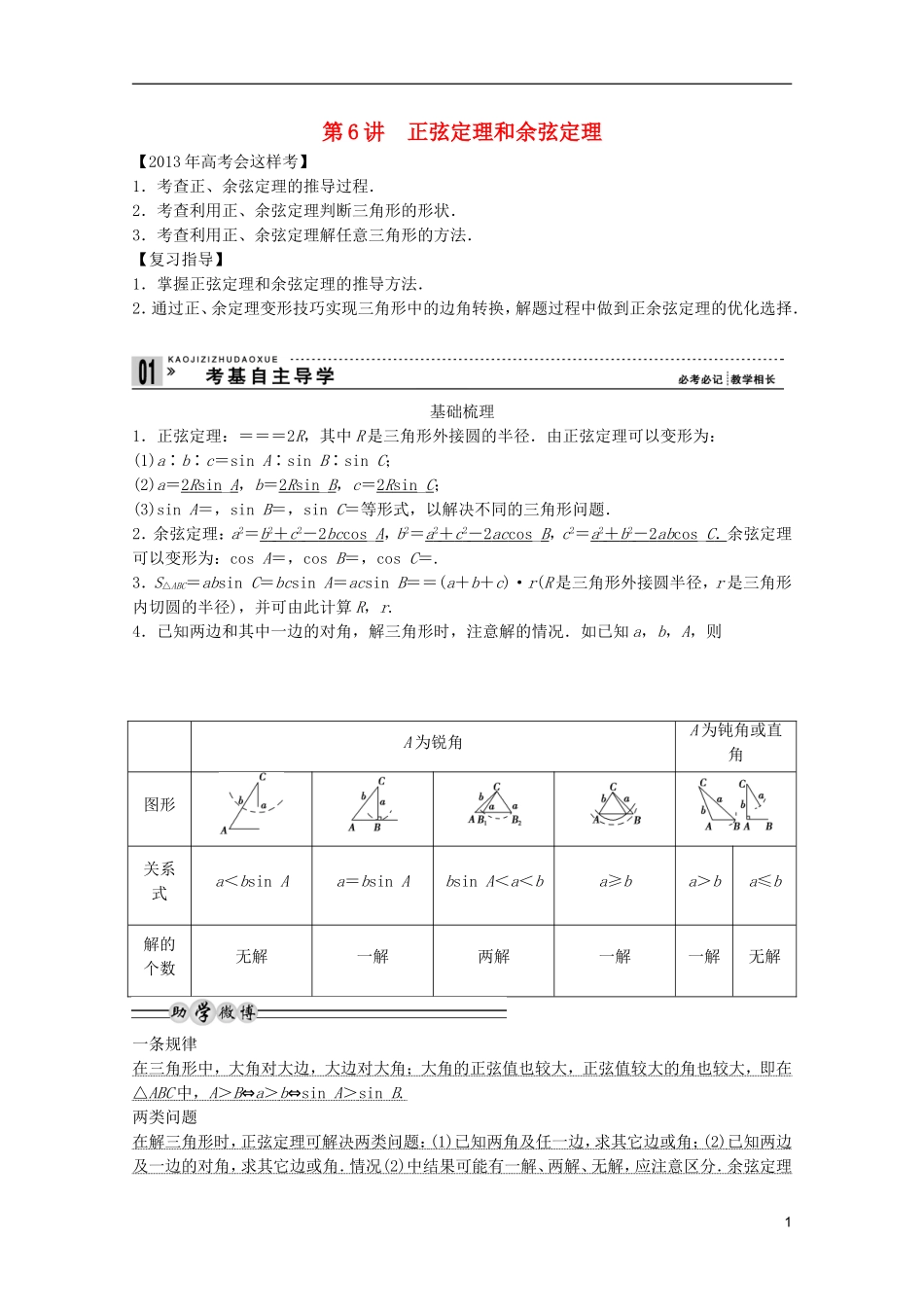
第 6 讲 正弦定理和余弦定理【2013 年高考会这样考】1.考查正、余弦定理的推导过程.2.考查利用正、余弦定理判断三角形的形状.3.考查利用正、余弦定理解任意三角形的方法.【复习指导】1.掌握正弦定理和余弦定理的推导方法.2.通过正、余定理变形技巧实现三角形中的边角转换,解题过程中做到正余弦定理的优化选择. 基础梳理1.正弦定理:===2R,其中 R 是三角形外接圆的半径.由正弦定理可以变形为:(1)a∶b∶c=sin A∶sin B∶sin C;(2)a=2 R sin _A,b=2 R sin _B,c=2 R sin _C;(3)sin A=,sin B=,sin C=等形式,以解决不同的三角形问题.2.余弦定理:a2=b 2 + c 2 - 2 bc cos _A,b2=a 2 + c 2 - 2 ac cos _B,c2=a 2 + b 2 - 2 ab cos _C . 余弦定理可以变形为:cos A=,cos B=,cos C=.3.S△ABC=absin C=bcsin A=acsin B==(a+b+c)·r(R 是三角形外接圆半径,r 是三角形内切圆的半径),并可由此计算 R,r.4.已知两边和其中一边的对角,解三角形时,注意解的情况.如已知 a,b,A,则A 为锐角A 为钝角或直角图形关系式a<bsin Aa=bsin Absin A<a<ba≥ba>ba≤b解的个数无解一解两解一解一解无解一条规律在三角形中,大角对大边,大边对大角;大角的正弦值也较大,正弦值较大的角也较大,即在△ ABC 中, A > B ⇔ a > b ⇔ sin A > sin B . 两类问题在解三角形时,正弦定理可解决两类问题: (1) 已知两角及任一边,求其它边或角; (2) 已知两边 及一边的对角,求其它边或角.情况 (2) 中结果可能有一解、两解、无解,应注意区分.余弦定理 1可解决两类问题: (1) 已知两边及夹角求第三边和其他两角; (2) 已知三边,求各角. 两种途径根据所给条件确定三角形的形状,主要有两种途径:(1) 化边为角; (2) 化角为边,并常用正弦 ( 余弦 ) 定理实施边、角转换. 双基自测1.(人教 A 版教材习题改编)在△ABC 中,A=60°,B=75°,a=10,则 c 等于( ).A.5 B.10 C. D.5解析 由 A+B+C=180°,知 C=45°,由正弦定理得:=,即=.∴c=.答案 C2.在△ABC 中,若=,则 B 的值为( ).A.30° B.45° C.60° D.90°解析 由正弦定理知:=,∴sin B=cos B,∴B=45°.答案 B3.(2011·郑州联考)在△ABC 中,a=,b=1,c=2,则 A 等于( ).A.30...